SIMPLE GEOMETRY IN COMPLEX ORGANISMS

Journal of Bodywork and Movement Therapies

 2010;14:424-444. ^link

Graham Scarr     ^{request copy}

ABSTRACT

Many cultures throughout history have used the regularities of numbers and patterns as a means of describing their environment. The ancient Greeks believed that just five archetypal forms – the ‘platonic solids’ – were part of natural law, and could describe everything in the universe because they were pure and perfect. The formation of simple geometric shapes through the interactions of physical forces, and their development into more complex biological structures, supports a re-appreciation of these pre-Darwinian laws. The self-assembly of molecular components at the nano-scale, and their organization into the tensegrities of complex organisms is explored here. Hierarchies of structure link the nano and micro realms with the whole organism, and have implications for manual therapies.

KEYWORDS: crystallography, helix, icosahedron, natural law, platonic solids, symmetry, structural hierarchies, tensegrity, tetrahedron

INTRODUCTION

Many cultures throughout history have used the regularities of numbers and patterns as a means of describing their environment. The ancient Greeks believed that just five archetypal forms – the ‘platonic solids’ – were part of natural law and could describe everything in the universe because they were pure and perfect (fig.1)^{Fuller 1975 sec.820.00}.

This platonic conception of nature persisted up until the mid nineteenth century when Charles Darwin published his revolutionary ‘Origin of Species’, “After Darwin the whole lawful scheme was overthrown and organic forms came to be seen as contingent mutable assemblages of matter – ‘clever artifact like contrivances’ – put together gradually during the course of evolution primarily by natural selection for biological function”.^{Denton et al 2003} A recognition of natural patterns and shapes derived from physical laws seemed to reassert itself in 1917 when d’Arcy Thompson published his classic ‘On Growth and Form’,^{Thompson 1961} but in the scientific mainstream this remained little more than interesting. Using simple geometry to describe a complex organism is likely to generate a certain of skepticism, as esoteric and occult descriptions seem rather simplistic compared to modern scientific thinking. However, in 1928 Frank Ramsey proved that every complex or random structure necessarily contains an orderly substructure. His proof established the fundamentals of a branch of mathematics known as Ramsey theory, which is used to study the conditions under which order must appear, such as in large communication networks and the recognition of patterns in physical systems. The theory suggests that much of the essential structure of mathematics consists of extremely large numbers (with very complicated calculations) derived from problems which are deceptively simple.^{Graham & Spencer 1990; Fuller 1975 sec.227.00} From the perspective of the human body, Ramsey theory implies that simple shapes might form part of that underlying substructure, and an examination of how these could arise through the interactions of physical forces is presented. This supports recent research which reinstates physical law, and not natural selection, as the major determinant of biological complexity in the sub-cellular realms.^{Denton et al 2003} The development of these shapes into more complex structures, and how they model biology, with implications for manual therapy then follows.

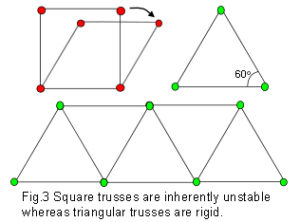One of the problems that nature seems to solve repeatedly is that of the most efficient ways of packing objects close together. A circle drawn on a piece of paper, ie. in two dimensions (2D), demonstrates this. The circle encloses the largest area within the minimum boundary, which makes it a ‘minimal-energy’ shape (requiring the least amount of energy to maintain). Circles enclose space, as well as radiate out into it, as can be seen in a drop of oil floating on water, the growth of fruit mould, and the ripples in a pond. However, this efficiency is severely compromised when several circles are put next to each other as gaps are left in between (fig.2). Other shapes, such as squares and triangles will both fill the space completely, but the proportion of area to boundary is not as good as with the circle. A square is inherently unstable; while triangles are very stable, even with flexible joints (fig.3). Structures that are not triangulated can generate torque and bending moments at their joints, and must be rigidly fixed to prevent them from collapsing.
Soap bubbles spontaneously join together with outside surfaces that meet at 120^o, just like hexagons, whether the bubbles are equal in size or not (fig.6). This is because soap molecules hold together through their surface tension, which tries to mi
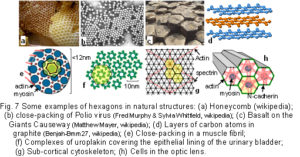
nimize itself and reduce the surface area. ^{(Fuller 1975 sec.825.20; Stewart 1998 p16} Some examples of naturally occurring hexagons are shown in fig.7.^{Bassnett et al 1999}

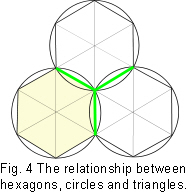
All this would seem to make the triangulated hexagon the obvious choice for close-packing in two dimensions. In 3D, however, a structure which fulfills the same purpose may not be so readily apparent. The ancient Greeks recognised the importance of the five regular polyhedra because of their intriguing properties (Fig.1).^{Fuller 1975 sec.820.00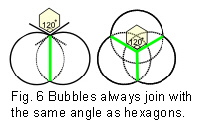} Their outer faces are made from shapes which are all the same; a sphere circumscribed around each one will touch all the corners, while one inscribed within will touch the centre of all the faces; and they all have 3, 4 or 5 sides. Joining up the face centres creates the ‘dual’ of that shape, ie the octahedron and cube are duals of each other; and the dodecahedron and icosahedron similarly; the tetrahedron is unique in that it is a dual of itself. Not a hexagon in sight… yet!

Just as the circle is the most efficient shape for enclosing space in 2D, so its equivalent in 3D is the sphere. Atoms, bubbles, oranges, and planets all approximate to spheres. Putting lots of spheres next to each other still leaves all those wasteful spaces in between, just like the circles did; but there is a more efficient solution. In order to tease out some of the consequences of packing spheres closely together, plastic balls have been glued together (fig.8). The same arrangements are also shown as lattices of steel balls, with coloured magnetic sticks representing the inherent ‘minimal-energy’ characteristic of close-packing (ie their centres of mass are at the minimum possible distance apart).^{Connelly & Back 1998} Adding more spheres to a particular shape creates higher-order structures of the same shape, numbered according to the [magnetic] connections on their outer edge (fig.8).^{Fuller 1975 sec.415.55}

Tetrahedron

The simplest and most stable arrangement of spheres in 3-D is a tetrahedron, because of its triangles.^{Fuller 1975 sec.223.87} Methane and ice molecules configure as tetrahedrons; a pile of oranges and grains of sand are rough tetrahedrons; and in the early embryo, four cells arrange as a tetrahedron. Adding more spheres to the tetrahedron produces higher order structures and the emergence of another shape – the octahedron.

Octahedron (fig.9)

The octahedron appears as an inevitable consequence of close-packing. It is naturally found in radiolarian structures, ^{Fuller 1975 sec.203.09}
and is the basis of the octet truss used by structural engineers because of its stability. It does have 3 equatorial squares at 90^o to each other, but their stability is maintained because of the triangles at each vertex.^{Fuller 1975 sec.420.01} A good approximation of this truss appears in the bones of birds, probably due its strength and lightness.^{Thompson 1961 p 236}

Cuboctahedron (fig.10-12)

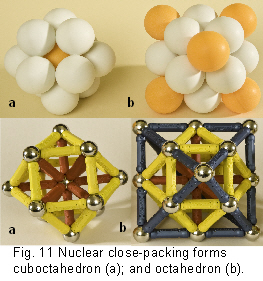
Increasing the tetrahedron to its 4^th order (figs.8;10) produces the first close packing of spheres around a central nucleus, and the emergence of another shape – the cuboctahedron (which is not a platonic solid).^{Fuller 1975 sec.414.00} This  shape is also contained within a 2^nd order octahedron (fig. 11).

Cube

The addition of a tetrahedron to each of the 8 triangular faces of the 2^nd order cuboctahedron turns it into a cube, or looking at it another way, the cuboctahedron is a cube with the corners cut off. If these were cut away further, it would end up as an octahedron. When four corners of a cube are connected diagonally, they enclose a 4^th order tetrahedron (fig.13b).

The cuboctahedron and cube are not shapes which generally appear in biological structures, but they are still relevant to the discussion. Table 1 shows a comparison of the relative volumes of these shapes when taking each one as unity. It can be seen that the volume of the tetrahedron is the only standard where all the others can be expressed as integers; the other comparisons leave awkward fractions or irrational numbers which disguises their simple relationships. Man-made structures commonly use cubes with their 90^o angles, but these shapes are relatively rare in the natural world where they are constructed from discrete components, and 60^o geometry is more prevalent – an observation noted by Buckminster Fuller.^{Fuller 1975 sec.410.10} An architect of some renown, he formulated a complete system of geometry based on 60^o, which applied to a wide diversity of the laws formulated in physics and chemistry.

Tetrahedron	Octahedron	Cube	Cuboctahedron
1	4	6	20
0.25	1	1.5	5
016666…	0.6666…	1	3.3333…
0.05	0.20	0.30	1

Table 1. A comparison of the relative volumes of different shapes with the same edge length, when taking each one as unity.

In crystallography, for example, two basic types of close-packing are described – cubic (fig.14a) and hexagonal (fig.14b^{).Read 1974 p21} The different ‘layers’ are described as parallel to the surface of a cube, but as already shown, the value of this shape as a standard in nature is dubious. In ‘cubic’ close-packing, the true layers are at 60^o to the surfaces of the cube, and all the energy bonds in these layers are oriented in the same directions (fig.13) (This can be observed in the external angles of the hexagon in fig. 13c,which are 60^o). In ‘hexagonal’ close-packing, however, every third layer is rotated by 60^o around an axis perpendicular to the layer plane, and it doesn’t then produce simple shapes like those already described. 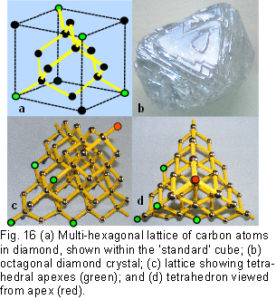In any case, there are plenty of hexagons in ‘cubic’ close-packing (figs.13c;15), and the tetrahedron, octahedron, cuboctahedron and cube are all examples of this.^{Read 1974 p96}
To illustrate this, diamond (the hardest natural substance) is constructed from carbon atoms arranged in a 3-D hexagonal lattice; with complete hexagonal rings that form tetrahedral units; which crystallizes as an octahedron; and uniquely has maximal cubic symmetry (fig.16)(all these polyhedra have cubic symmetry).^{Read 1974 p83; Sunada 2008}

All these shapes naturally occur as inorganic crystals, and there is no suggestion that they can literally be observed in the human body. This description, however, includes them in a unified and comprehensive approach to understanding natural forms, which are all influenced by the same energy-efficient ways of packing objects of similar size through the interactions of molecular forces.

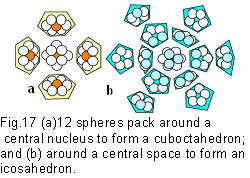Before getting to more complex structural mechanisms, it is necessary to make a brief return to the cuboctahedron, where it will be noticed that it is constructed from 12 spheres that create four interlocking hexagons around a central nucleus (figs.10;11;17a). Pauling (1964) described it as a ‘coordination polyhedron’ because its minimal-energy configuration is the common denominator of the tetrahedron, octahedron and cube. Fuller ^{(1975 sec.430.00)} considered the links between spheres as energy vectors, and called it the ‘vector equilibrium’. This shape has radial and circumferential vectors which are all the same size. In terms of vectorial dynamics, the outward radial thrust from the nucleus is exactly balanced by the circumferentially restraining chordal forces (figs.10;11). So, as well as the highest degree of symmetry (cubic), we have a coordinating shape (cuboctahedron) and a balance of forces (vector equilibrium), the significance of which will be explained later.

It is even possible to pack spheres tighter and at a lower energy level by removing the nucleus. This allows 12 spheres to compact differently around a smaller central space as 12 interlocking pentagons (figs.17b;18a;b). Joining all the spheres together creates an icosahedron – another platonic solid, but this one is different (fig.18c). Adding more spheres to the outside will not create a higher order, like in the previous shapes, because the spheres won’t all touch (fig.18d). A 2^nd order icosahedron won’t close-pack around the basic shape, or a 3^rd order around a 2^nd, because they would be unstable (figs.18e;f), and can only exist in their own right as a single outer shell. The icosahedron enlarges by subdividing each of its faces into more triangles, which is why it remains stable (fig.18g)(The relative volume compared to the tetrahedron in table 1 is 18.51).

In order to understand the full significance of simple geodesic geometry, we must look at another way that the universe uses to deal with complexity, namely, integration.

TENSEGRITY

The concepts of tensegrity [tensional integrity] have become increasingly recognized over the last thirty years as a useful model for understanding some of the structural properties of living organisms. Their appreciation follows from investigations in the 1940’s by Kenneth Snelson (website) who constructed sculptures with parts that appeared to defy gravity and float in the air. His structures greatly impressed the architect Buckminster Fuller (1975), that he incorporated them into his developments in structural design and set about exploring the principles underlying their formation. Fuller described two aspects of  geodesic geometry based on the icosahedron and referred to them as the geodesic dome and tensegrity.

[Fuller actually considered them as two aspects of the same thing, which has caused a great deal of confusion ever since, and the following should be considered in this way. He had a habit of making grand statements that obfuscated the details of what he was trying to say and many hours of discussion have been spent on trying to unpick these.]

The Geodesic Dome

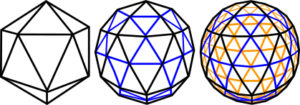The outstanding feature of geodesic domes is that they have a rigid external frame maintaining their shape, made from multiple struts or trusses arranged in geometric patterns. These are usually triangles, pentagons or hexagons, with triangulated structures being the most stable. The term ‘geodesic’ actually refers to the shortest path between two points (equivalent to the struts), so strictly speaking this definition should only refer to the triangulated structure. Aside from this, the ‘geodesic’ dome can enclose a greater volume with minimal surface area, with less material than any other type of structure apart from a sphere. When the diameter of a sphere doubles, the surface area increases 4 fold and the volume 8 fold, which makes such structures very efficient in terms of construction material. The 1^st order tetrahedron and octahedron are geodesic structures which enlarge by adding more spheres to the outside, but they then cease to be hollow structures. In contrast the icosahedron, whose spheres enclose a small central space, creates an outer geodesic shell which enlarges by adding more triangular faces within it (figs.18g;19). The icosahedron has several attributes that are advantageous for biological structures.^{Levin 1995} It is the closest of all the regular polyhedra to being spherical – making it efficient in terms of construction material; and it is fully triangulated – giving it stability. It has 12 vertices, 20 triangular faces and 30 edges, with five faces and their edges meeting at each vertex; and demonstrates six 5-fold, ten 3-fold and fifteen 2-fold symmetries

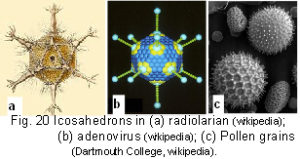Fuller introduced his geodesic domes during the 1950’s; and because their strength increases as they get bigger, it has been possible to build some very large structures. Some of these can be seen in the Eden project in Cornwall, and protective coverings on radar installations. Some natural structures are: ‘Buckyballs’ – a form of carbon named after Fuller – with 60 atoms linked together to form 20 hexagons, interspersed with 12 pentagons – the same as the pattern on a football (actually a spherical truncated icosahedron); viruses; the silica shells of radiolaria; pollen grains; clathrins (endocytic vesicles beneath the cell membrane); and the cellular cytoskeletal cortex (fig.20).

In 1956, Crick and Watson, the discoverers of DNA, pointed out that the only way to build a hollow protein shell out of identical subunits is a shape with cubic symmetry. Since then it has been amply confirmed that the icosahedron is the best shape for producing the outer capsid shell of the ‘spherical’ viruses, because it is a minimum free-energy structure, and spontaneously assembles through the actions of intermolecular forces (fig.20b).^{Crick & Watson 1956; Kushner 1969; Caspar 1980; Van Workum & Douglas 2006} These viruses form larger structures, which get even closer to a sphere, by using more protein subunits (capsomers) to subdivide their triangular faces (fig.19). The maximum number of identical subunits which can be arranged is 60, and to become larger, some subunits must distort slightly in order to form stable bonds. This ‘quasi-equivalence’ is necessary for preserving the icosahedral template, with multiples of 60 subunits allowing many more triangular faces, but there are always just 12 vertex pentagons (it is the 5-fold symmetry which creates the geodesic dome).^{Caspar 1980} (The icosahedron has also been found to play an important part in the structure of many electron-deficient substances, including metals and alloys.^{Pauling 1964,1990; Teo & Zhang 1991}

Multiple icosahedra can arrange neatly together in a thick planar sheet because of their hexagonal outline (figs.7b;18c), making the hexagon the link between space filling in 2D and the icosahedron in 3D. They can stack in a column or helix; branch or pack around each other (incompletely) to create curved surfaces; and form more complex patterns and shapes in 3D (fig.21).

In contrast, tetrahedral and octahedral based trusses are not omnidirectional in form and function; they have a smaller volume to surface area ratio; they do not close-pack at all well and their shapes do not self-generate. Cubes and dodecahedra are also inherently unstable unless they are triangulated, but will not be considered further at this point. However, they are still significant to later discussion.

Applying pressure to any point of a geodesic dome causes force to be transmitted around the edges, with both compression and tension operating within different parts of each strut, which means that they must be made of a material that can deal with both types of loading. Tensegrities, on the other hand, have these two components separated, optimizing the material properties of each.^{Ingber 2003a}

Tensegrity

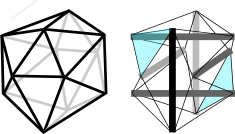The description of biological structures as tensegrities first appeared in the literature in the early 1980’s, with independent contributions by Donald Ingber^{Ingber et al 1981} and Stephen Levin.^{Levin 1982} Tensegrities consist of a set of struts under compression, and an arrangement of cables under isometric tension. The resultant pull of the cables is balanced by the struts, providing structural integrity with the compression elements appearing to float within the tension network. A load applied to this type of structure causes a uniform increase in tension around
all the edges and distributes compression evenly to the struts, which remain distinct from each other and do not touch.^{Skelton et al 2001; Masic et al 2006} Fuller described it as: “…continuous tension and discontinuous compression”.^{Fuller 1975 sec.700}

The geodesic dome icosahedron can be converted into a tensegrity structure by using six new compression members to traverse the inside, connecting opposite vertices and pushing them apart (fig.22).^{Fuller 1975 sec.700; Levin 1982} The edges can then be replaced with cables so that the outside is entirely under tension. (Some of the edges have disappeared in the transition to tensegrity because they are now redundant and not essential to the new structure.)

To summarize the significant aspects of this type of design:^{der Veen 2003}

1. Stability – achieved through the configuration of the whole network, and not because of the individual components. It is also omnidirectional, with the different elements maintaining their respective properties regardless of the direction of applied load.

2. Balance – the tension and compression components are separated and balanced mechanically throughout the entire structure, which will optimize automatically so as to remain inherently stable.

4. Energetically efficient – giving maximum stability for a given mass of material. In mechanical terms it cannot be anything other than in a balanced state of minimal energy throughout.^{Masic et al 2006; Skelton et al 2001}

Since its discovery, the tensegrity concept has developed in four main areas – sculpture;^Snelson building (Fuller); space research and structural biology. Space research has shown a great deal of interest in tensegrities because of their lightness and other unusual structural properties. Defining their complex mathematics will probably lead to new developments in biological research, with physical and computerized modelling becoming valuable tools for exploring their potential in the future.^{Connelly & Back 1998; Skelton et al 2001; Coughlin & Stamenovic 2003; Masic et al 2006; Yu et al 2008}

The geodesic dome has been considered distinct from tensegrity for the purpose of description so far – one has all the struts touching, and the other has them all separated; although tension maintains their integrity in both cases, and they are really both prestressed.^{Fuller 1975 sec.703.03} They seem to be poles at opposite ends of a continuum, although even this distinction is an illusion, as will be explained. A definition which satisfies all researchers has so far remained elusive, because some aspects relating to mechanical engineering do not apply to biology, and the following examples use a broad and inclusive approach.
In contrast, the molecular dynamics within living organisms are in continuous flux, as conflicting forces attempt to resolve themselves. Eventually they can settle into a balanced and stable state of minimal-energy, at least until some other force exerts its influence. Tensegrities are a most attractive proposition in living systems, because they create an energy ‘sink’ for the interacting force fields (a ‘basin of attraction’ in dynamics terminology), and make possible an enormous number of flexible and stable structures through changes in the lengths of their compression members.^{Connelly & Back 1998; Skelton et al 2001; Nelson et al 2005; Ingber 2006a,b,2008}
Their non-linear stress-strain relationship is an essential aspect of biological materials where it has been related to the differing properties of components in their nano and micro structures (figs.24;29);^{Gordon 1978 p164; Lakes 1993; Skelton et al 2001; Puxkandl et al 2002; Gao et al 2003; Gupta et al 2006} one of the smallest of these is the helix.

The Helix

The helix is a series of curves which all have the same radius, drawn out like a long spring (figs.24-29). Probably the most famous of all is DNA – deoxyribonucleic acid – a double helix of two chains running in opposite directions. The discoverers of DNA rightly predicted that helixes would be one of the simplest of shapes to spontaneously assemble through inter-molecular forces.^{Crick & Watson 1956; Kushner 1969; Caspar 1980; Van Workum & Douglas 2006}
Biological helixes are stabilized through a balance between the attraction (tensional) and repulsion (compressional) forces within the molecule, which makes them tensegrities in their own right. They can also flex without buckling, lengthen without breaking, and are capable of rotation without deformation.^{Stecco 2004}  All known filamentous viruses are helical (most of the rest are icosahedral) fig. 20b;21c).
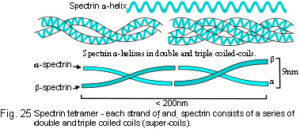
In proteins, sequences of amino acids can fold into helixes and further twist around each other to form double or triple coiled-coils (super-coils)(fig.25), or fold with other helixes (or β-sheets) to form globular structures. Of the huge number of possible amino acid combinations, protein folding is limited to a set of about 1000 different forms because of some basic self-assembly rules, analogous to the laws of chemistry or crystallography, which correspond to an energy   minimum.^{Denton et al} 

The Cytoskeleton

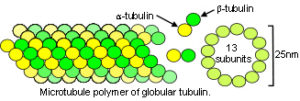
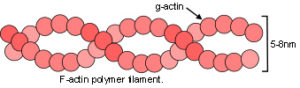Within the cytoplasm, the prestressed cytoskeletal lattice consists of microtubules – tightly packed helices of globular tubulin protein under compression (fig.26); microfilaments – double helices of the protein F-actin under tension (fig.27); and helical protein intermediate filaments which stabilize and integrate the whole structure, from cell membrane to the nucleus.^{Ingber 2008; Brangwynne et al 2006; Maguire et al 2007} Experimental support for the cytoskeleton as a tensegrity structure now seems overwhelming^{Ingber 2008} although some studies have been unable to confirm it.^{Heidemann et al 1999; Ingber et al 2000}

The Cellular cortex

The cellular cortex is essentially made from triangulated hexagons of the helical protein spectrin (fig.25), coupled to underlying bundles of the helical protein actin (figs.7g;27).^{Liu et al 1987; Weinbaum et al 2003; Li et al 2005; Zhu et al 2007} The erythrocyte, with a diameter of 8µm, has a composite membrane which distorts as it flows through smaller capillaries, but allows the cell to recover its biconcave shape. The network is organized into ~33,000 repeating units, each with a short central actin protofilament linked by 6 spectrin filaments under tension, to a lipid-bound suspension complex.^{Sung & Vera 2003; Zhu et al 2007} About 85% of these units appear as hexagons, with ~3% pentagons and ~8% heptagons, which suggests that the hexagonal arrangement is a preference, and not perfect (Liu et al 1987). The erythrocyte membrane may be considered as many tensegrity actin/spectrin units within a geodesic dome, which is itself a bilayered structure of phospholipid molecules with outer heads under tension separated by hydrophobic tails under compression. It has also been modelled around an icosahedron.^{Li et al 2005} Deformation of the membrane network may cause turbining of the actin protofilaments through the suspension mechanism, thereby facilitating oxygen transfer from one side of the membrane to the other.^{Sung & Vera 2003; Zhu et al 2007}

This arrangement of different components at varying size scales is a common feature in biology, where the functions of each one contribute to a higher collective function within a hierarchy of structures (figs.24;29).

Structural Hierarchies

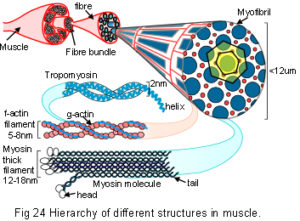
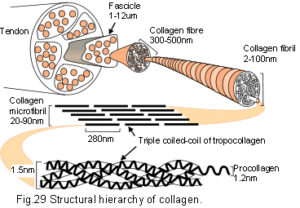
The nano-structures of collagen and spider silk have both been described as tensegrities^{Skelton et al 2001} within a hierarchical fibrous structure (fig.28).^{Termonia 1994; Knight & Vollrath 2002; Du et al 2006} Collagen, the most abundant structural molecule based on the helix, is the main constituent of the extracellular matrix, fascia, tendons and ligaments. More than twenty different types have been described in different tissue specific combinations which are particularly able to resist tensional stresses. At the nano-scale three helical procollagen polymers wind around each other to form a triple helix of tropocollagen. These molecules then arrange laterally in a quasi-hexagonal configuration with cross-linking to form collagen microfibrils, and pack sequentially in a hierarchy to form a subfibril, fibril and collagen fibre (fig.29).^{Jager & Fratzl 2000; Puxkandl et al 2002; Gao et al 2003; Gupta et al 2006; Perumal et al 2008}

Collagens and spider silk are also examples of liquid crystal elastomers – different states, or mesophases of matter, that lie between liquids and solid crystals.^{Ho et al 1996; Knight & Vollrath 200} They are flexible and malleable, with fibres that show a high degree of orientational order and varying degrees of translational order, and are sensitive to mechanical loading and changes in electro-magnetic fields; which may influence their synthesis and define fibre orientation during morphogenesis and tissue remodelling. Even though spider web fibres are secured at their ends to what is effectively a continuous compression component, the whole web has been classed as a tensegrity on structural engineering grounds (fig.28).^{Connelly & Back 1998}

Fractals

The self-similar geometrical structure of collagenous tissues has been demonstrated in the fractal-like character of their polarization properties, with degenerative-dystrophic changes revealed by alterations in these properties.^{Ho et al 1996; Angelsky et al 2005} This observation may be of value in pre-clinical pathological diagnostics, and a correlation between these findings and tissue palpation would be useful research in the future. Fractal analysis is commonly applied to natural structures, where similar shapes and patterns appear at different size scales, linking hierarchies throughout the body.^{Mandelbrot 1983; Skelton et al 2001; Jelinek et al 2006} The branching patterns of blood vessels, the bronchial tree and nerve fibres all display this property.^{Zamir 2001; Pelagyia et al 2006; Phalen et al 1978; Thomas et al 2005} These characteristic shapes are developmental remnants of nonlinear dynamic systems which were sensitive to small changes in the local environment, created instabilities in growth and caused the typical branching pattern which extends from the micro to the macro scale. They are part of ‘deterministic chaos’ or chaos theory.^{Goldberger et al 1990}

The Matrix

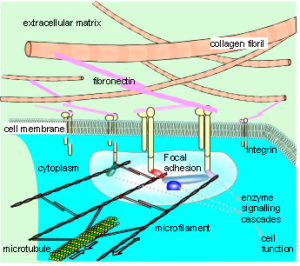The extracellular matrix, surrounding virtually every cell in the body, provides a branching structural framework which extends through the fascia to the whole organism. It attaches to the cellular cytoskeleton through adhesion molecules in the cell membrane, allowing a transfer of mechanical forces between them and changes in the cytoskeletal tension.^{Ingber 2003a,b,2008} Multiple intra-cellular signalling pathways are activated as a result which provide multiplexed switching between different states such as cell growth, differentiation or apoptosis. Conversely, local tensional stresses within the cytoskeleton transfer to the extracellular matrix and produce effects on other cells at some distance. Long-distance transfer of mechanical forces between different tissues could then spatially orchestrate their growth and expansion, allowing complex multi-cellular tissue patterns to emerge through interactions among a hierarchy of different components.

Multi-modular hierarchies of form and function can thus be linked, with simplicity evolving into complexity, and the whole system mechanically functioning as a unit.^{Stecco 2004 p25; Nelson et al 2005; Ingber 2006a,2008; Parker & Ingber 2007} As a self-organizing tensegrity construction system, the matrix could repair and replace itself at a local level, by allowing small and incremental changes compatible with the mechanical demands of all its components. Stecco (2004 p31) described the fascia as a tensioned network which may coordinate the motor system in a way that the central nervous system is incapable of.

Modelling Icosahedral Tensegrities

The icosahedron is particularly useful in modelling the tensegrities of biological structures, because it demonstrates both geodesic dome and tensegrity properties which can be connected to form an infinite variety of shapes (figs.21;23;31). Even the tension and compression elements can be made from interlinked icosahedra, themselves constructed from smaller icosahedra, repeating further in a self-similar structural hierarchy.^{Fuller 1975 sec.740.21; Ingber 2003a; Levin 2007} Curved compression elements differ from straight struts (fig.22) because their outer convex surfaces are under tension and their inner concave surfaces are under compression. Biological materials deal with both types of loading by separating them into nano and micro structures within a hierarchy.^{Gordon 1978; Lakes 1993; Puxkandl et al 2002; Gao et al 2003; Gupta et al 2006; Brangwynne et al 2006} Inferences that this is ultimately due to their tensegrity construction have been made.^{Skelton et al 2001; Levin 2007; Ingber 2008} In addition, when spheres are added to the outside of an icosahedron they do not close-pack completely, and an instability develops (figs.18d-f;21a). This apparent ‘flaw’ in the packing arrangement allows another possibility for modelling an infinite variety of shapes, as different parts of the structure branch outwards, and the spaces in between can fill with smaller icosahedra.

It may now be seen that the distinction between geodesic dome and tensegrity is really just relative to the scale at which they are observed, a corollary which should be added to any definition. Even the close-packing of atoms (spheres) should be considered as a ‘tensegrity with invisible struts’ because their centres of mass are held a minimum distance apart.^{Connelly & Back 1998} Distinctions of structure and function in biology may essentially be points on a continuum and artefacts of textbook classification. Although geodesic domes appear limited to the cellular size level, tensegrities almost certainly dominate beyond this. At the macro scale the fascia, muscles, ligaments and capsules provide the tension; while the bones and tissue bulk of muscles, organs and fluid-filled vessels resist compression.

Tensegrities within Tensegrities

Levin was the first to describe the higher complexities of the human body in terms of tensegrity, using the analogy of a bicycle wheel, where the compression elements of the central hub and outer rim are held in place by a network of wire spokes in reciprocal tension.^{Levin 1997,2005a; Connelly & Back 1998} This type of wheel is a self-contained entity, maintained in perfect balance throughout, with no bending moments or torque, no fulcrum of action, and no levers (fig.30). He suggested that the scapula may function as the hub of  such a wheel, in effect as a sesamoid bone, and transfer its load to the axial skeleton through muscular and fascial attachments.^{Levin 1997,2005a}

The sterno-clavicular joint is not really in a position to accept much compressional load, and the transfer of compression across the gleno-humeral joint has been found to be at maximum only when loaded axially at 90^o abduction.^{Gupta & van der Helm 2004} As compression can only take place normal to the glenoid surface ie at 90^o (it is essentially a frictionless inclined plane), the joint must rely heavily on ligamentous and muscular tension in all other positions. A humerus hub model would function equally well with the arm in any position. Similarly, the ulna could be a hub within the distal humeral ‘rim’ of muscle attachments, where load bearing across the joint may be significantly tensional, allowing compressional forces to be distributed through a tensioned network, and the hand to lift loads much larger than would otherwise be the case (fig.31). In this respect, zero compression across the femur and meniscii has been observed during arthroscopy in an extended knee joint under axial loading in vivo.^{Levin 2005b}

The pelvis is also like a wheel with the iliac crests, anterior spines, pubis and ischia representing the outer rim; and the sacrum representing the hub, tied in with strong sacro-iliac, sacro-tuberous and sacro-spinous ligaments. Similarly, the femoral heads may function as hubs within the ‘spokes’ of the ilio-femoral, pubo-femoral and ischio-femoral ligaments.^Levin2007

Joint movements display helicoid motion around a variable fulcrum and this is demonstrated in the simple tensegrity elbow in figure 31, a physiological feature not found in most other models.

Omni-directionality

According to Wolff’s law, tensional forces remodel the bony contours and alter the positions and orientations of their attachments, contributing to the complexity of shapes apparent in the skeleton.^{Kushner 1940; Kjaer 2004} As part of a tensegrity structure, each attachment would influence all the others, distributing forces throughout the system and avoiding points of potential weakness;^{Skelton et al 2001; Masic et al 2006} in contrast to a pure geodesic chain or truss which is vulnerable to buckling (fig.21c). Such a mechanism would be an advantage in long-necked animals such as giraffes and dinosaurs, where the load from the head is distributed throughout the neck (fig.23).^{Levin 1982} The erect spine and bipedal weight bearing capability of humans has traditionally been viewed as a tower of bricks and compressed disc joints, transferring the body weight down through each segment until it reaches the sacrum, but this is a relative rarity amongst vertebrates. Most other species have little or no use for a compressive vertebral column, which is frequently portrayed as a horizontal truss and cantilever support system.^{Thompson 1961 p245; Gordon 1978 p239} As the main difference in vertebrate anatomies is in the detail, it seems reasonable to suppose that they have some structural properties in common.^{Levin 1982;2002} Tensegrities are omni-directional, i.e. they are stable irrespective of the direction of loading; and the spine, pelvis and shoulder all demonstrate this property (within physiological limits), enabling dancers to tip-toe on one leg, and acrobats to balance on one hand.

Continuums of structure

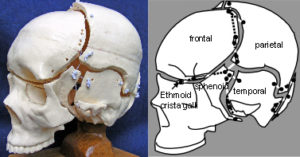Tensegrity and the geodesic dome may coexist at the same level within a particular functional unit and have been described in the cranium, where the bony plates of the vault substitute for curved compression struts and do not touch each other; alongside a more ‘geodesic dome’ cranial base (fig.32). Tension is provided by the dura mater – a tough membrane covering the brain – which regulates bone growth, maintains the separation of vault bones at the adjoining sutures, and integrates the whole structure into a single functional unit. It has been suggested that the brain influences the vault to grow outwards, through the dura mater, rather than physically pushing it out. ^{Scarr 2008}

Balanced mobility

Balanced and symmetrical tensegrities automatically assume the configuration that minimizes their stored elastic energy, with changes in shape that require very little control energy; in contrast to classical structures where significant energy is requi
red to work against the old equilibrium. ^{Skelton et al 2001; Masic et al 2006} Their high yield strain allows large shape changes to be accomplished at no loss in stiffness ^{Masic et al 2006} a distinctive feature in biological structures. The icosahedron has been described as an intermediary in a potential oscillating system ^{Fuller 1975 sec.460.08} with similarities to an energy efficient pump. ^{Levin 2002} If the vector equilibrium (cuboctahedron)(fig.11a) is constructed without radial vectors and joined with flexible connectors, and is compressed between two opposite triangular faces, it will contract and rotate symmetrically (due to the instability of the square faces) and assume the shape of the slightly smaller icosahedron (each of the square faces now becomes a rhomboid, or essentially, two triangles). Further compression causes the equator to twist and fold, and the structure transform itself through an octahedron, to the tetrahedron, and back again. The icosahedron is at the lowest energy state within the system, and the point around which changes in shape occur. Fuller called this mechanism the ‘jitterbug’.^{Fuller 1975 sec.460.00} An organism utilizing such a system would be able to move with the minimum of energy expenditure, and remain stable whilst changing shape.

SYMMETRY AND NATURAL LAWS

The ability… to generate elaborate and beautiful forms… comes from a simple but fundamental principle which governs the deep structure of the physical universe: symmetry. …Albert Einstein…argued that truly fundamental laws of nature must be the same at all times and in all places: that is, the laws must be perfectly symmetric… Principles of symmetry govern the four forces of nature (gravity, electro-magnetism, and the strong and weak nuclear forces that act between fundamental particles).” ^{Stewart 1998 p38}

The ubiquitous nature of symmetry offers a simple explanation for stable crystal lattices and other regular patterns, because of the balance of forces. Instabilities in the dynamics of living systems also generate complex patterns and shapes within hierarchies of structure, as self-similar shapes (fractals) scale up through dilation – one of the four principal types of symmetry transformation.

“Instability breaks the overall system symmetry, but it appears to be a localized fissure that is offset by…a balancing asymmetry elsewhere in the system. Essentially, the sum of all the asymmetries is symmetrical…Thus, we have patterns of symmetry that reflect the underlying symmetrical nature of the universe, and patterns (and forms) that are generated by instabilities in the system.”  ^{Kreigh& Kreigh 2003}

That different structures should emerge at different levels in complex organisms is typical of evolutionary selection. Over hundreds of millions of years chance mutations in the genetic code occasionally gave rise to new characteristics which conferred an advantage to the organism, whilst existing traits which remained useful were retained, through natural selection. This bifurcation in development creates asymmetries which must be balanced in order to permit new higher order symmetries.^{Stewart 1998 p 114}

Organization is still part of the self-assembly capacity, but the resulting form may have a very different appearance from its component substructures (figs.24;29) “…and be arranged into almost any contingent artefactual arrangement we choose”.^{Denton et al 2003} Correlations with ‘60^o geometry’ at the macro scale may then be more coincidental; ^{Phalen et al 1978; Thomas et al 2005} and description such as ‘close-packing of the knee in full extension’ means something different to ‘close-packing of spheres’.

SUMMARY

The tetrahedron is one of the simplest of shapes in 3-D because of its close-packing efficiency, minimal-energy configuration and triangular stability. It gives rise to the octahedron and square in the octet truss, and nuclear close-packing in the cuboctahedron and cube; all manifesting within each other, and all resulting from ‘60^o geometry’. The hexagon, and cubic symmetry of these shapes links them to the polyhedron most suited to fulfill structural evolution in biology, which is the icosahedron, possibly part of the substructure predicted by Ramsey. ^{Graham & Spencer 1990} All these polyhedra undergo a phase transition as they morph into tensegrity structures, giving endless shape possibilities, but their well defined geometries are now obscured. The cuboctahedron links them to the ‘vector equilibrium’ and dynamic ‘jitterbug’, where energy efficient transformations of shape become significant. Self-assembling helical proteins carry the tensegrity principle into the nano-structures of the cell and extracellular matrix; and through structural hierarchies to the whole body. The genes orchestrate a battery of physical and chemical processes, but the natural laws of physics still provide the construction rules^{Stewart p 25; Denton 2003; Harold 2005; Ingber 2006b} where shape becomes determined more by Darwin’s “natural selection for biological function”.^{Denton et al 2003}

CONCLUSION

“…ideal geometries… pervade organic form because natural law favours such simplicity as an optimal representation of forces”. Stephen Jay Gould ^{Thompson 1961 xi} 

Energy consumption is the key to understanding the structural complexities of living organisms, and as energy-efficient structural mechanisms, tensegrities apply at every level from the atom to the whole body. The icosahedron links the simple geometry of the platonic solids to the tensegrities of complex shapes, and lends itself to their modelling. It also becomes a transient in energy-efficient transformations of shape, through the ‘jitterbug’ system described by Fuller.

As a tensioned tensegrity network, the fascia may have a coordinating function throughout the body; and as manual therapies make contact at the whole body level, it provides a pathway for therapeutic interventions right down to the molecular scale.

ACKNOWLEDGEMENTS

I wish to express my appreciation to Stephen Levin for information on the icosahedron which initiated this article, and to Nic Woodhead, Chris Stapleton and Andrea Rippe for the opportunity to discuss some of these concepts with helpful feedback. Also to Rory James for the photographs in figures 9-12 & 15.