Biotensegrity: concept, principles and applications. link
Graham Scarr 2025
In: Fraternali, F., and Rimoli, J. (Eds.) Tensegrity systems: basic concepts, mechanical metamaterials, biotensegrity . CISM International Centre for Mechanical Sciences. Springer Nature Switzerland; 151-174.
Abstract
Biotensegrity models living systems in ways that were inconceivable in the past but has taken some time to become widely accepted because of its challenges to generally accepted wisdom. Orthodox biomechanics has its origins in mechanistic models from the seventeenth century, and as a consequence, has allowed over-simplified representations of anatomy and motion to persist to the present day with the approximations and assumptions inherent within its methods routinely overlooked. In contrast, biotensegrity appreciates that the human body is NOT a machine but a complex heterarchical structure of intertwined relationships that result from a fundamental set of self-organizing principles. Here, the closed-chain kinematics of tensegrity provide a unified mechanical system that extends from molecules to the complete organism and represents a paradigm shift in thinking. A new classification of biomechanical models that includes super-stable tensegrity and has relevance to mechanical engineering in general is then introduced.
Keywords
Closed kinematic chains; energy-efficiency; Platonic solids; self-organization; super-stability; systems biology
1. Introduction
In 1944, Erwin Schrodinger asked the question “What is life?” and examined it in relation to the scientific knowledge available to him at the time, and many others have asked the same. In the process, Schrodinger recognized the shortcomings in conventional biophysical explanations and suggested that “we must be prepared to find a new type of physical law”, but after eighty years, how much closer are we to answering that question. Biology, as the scientific study of life, is a field of research that has long intrigued the human mind, and it is huge. Not only does it examine the form and development of an immense variety of different organisms, it also provides insights into their complex anatomies, mechanics and relationships at every level: from molecules and cells to adult populations and complex ecologies. Our understanding of living systems thus forms a body of knowledge that is probably unrivalled in any other sphere, and naturally a significant part of that research has been oriented towards improving the human condition and benefitted our healthcare systems in remarkable ways.
A deeper understanding of the mechanics of molecules, cells, tissues and their environments has led to developments in pharmacology that benefit us all, from simple pain killers to the treatment of life-threatening diseases. In-silico models provide valuable information that informs the development of new types of prosthesis and super-complex surgeries, while the involvement of tensegrity in the behaviour of cells, formation of cancers and the body as a whole has long been recognized (Kirkby, 1976; Robbie, 1977; Ingber et al., 1981; Levin, 1981).
However, current thinking about the human body is largely based on mechanistic models from the seventeenth century (Borelli, 1680; Piolanti et al., 2018), and as a result, has allowed over-simplified representations of anatomy to persist to the present day. Even though the dissections of Vesalius (Vesalius, 1543) were truly revolutionary in the sixteenth century, established traditions and the persistence of outdated methodologies have unwittingly constrained how we think about life (Nicholson, 2018; Levin and Lowell de Solórzano, 2024; Scarr et al., 2024).
Living organisms are hugely complex, fundamentally indeterminate and exist in states that are far from equilibrium (Glazier and Davids, 2009; Pascal and Pross, 2015), and as a consequence, they have been simplified in ways that have enabled great progress in the mapping of structure to function but obfuscated the foundational basis for stability, motion and life itself (Profeta., 2020; Scarr et al., 2024). As (Russell, 2009) p. 42) wryly noted, “All exact science is dominated by the idea of approximation”, which suggests that biomechanical models have yet to reach their full potential because much of the basic knowledge that currently underpins them is questionable.
Biotensegrity is a concept that challenges many traditional ideas because it recognizes that all living systems conform to some fundamental principles of self-organization and that these apply at every level from molecules to the complete organism (Levin, 2015; Kiely and Collins, 2016; Scarr, 2018). However, trying to explain its significance is not a straightforward process. The human body is NOT a machine, and like the tensegrity model (Figure 1), a reductionist examination of its constituent parts in isolation does not tell us much about the emergent properties of the whole (Levin and Lowell de Solórzano, 2024). As that old adage says: ‘Before embarking on a new field of study, make sure you understand it thoroughly first’, and which implies that it is necessary to have an appreciation of both the details and the complex picture at the same time; and as we have to start somewhere, this chapter examines the subject from several different perspectives. Certain aspects might then seem rather simplistic on their own but must always be considered in relation to the whole. As Levin put it: “Tensegrity is not an engineering principle that applies to biology, but a biological principle that can be applied to engineering” (Pers. comm. 2024).

Biotensegrity represents a completely different way of thinking about the human body — and all living systems — where stability and motion are controlled from within the structure itself and in synergy with the nervous system (where befits) (Kiely and Collins, 2016; Wilson and Kiely, 2016; Levin., 2017). The strength of individual ‘parts’ is then no longer the primary concern — as it is with engineering models — but rather the dynamic balance of invisible force vectors within them (Ingber et al., 2014; Kiely and Collins, 2016; Stamenović and Smith, 2020). It is thus important to note that the terms tensegrity and biotensegrity can mean different things that depend on the context, and the following will be a qualitative assessment of the concept – principles and mechanics – and its relevance to engineering in general.
2. Employed notation
This chapter considers discontinuous compression tensegrity structures as assemblies of cables that carry tensile forces, ‘floating’ struts that carry compressive forces, and bars that individually carry either tensile or compressive forces.
3. How we got to where we are now
Foundational to the modelling of human movement has been the work of (Borelli, 1680) who compared living organisms with man-made machines of the day and described the body as a system of levers, pulleys and other contrivances that are now part of mainstream thinking (Humphrey, 2003; Piolanti et al., 2018). In other words, a musculoskeletal duality of weight supporting columns, beams and arches with the bones stacked on top of one another like a pile of bricks and the soft-tissues moving them around like the rigging in a sailing ship; and such a system of rigid and stretchable elements that mechanically complement each other is naturally very appealing and computationally well-supported, but it also creates a problem (Levin, 2002; Scarr et al., 2024).
The stress/strain simplification
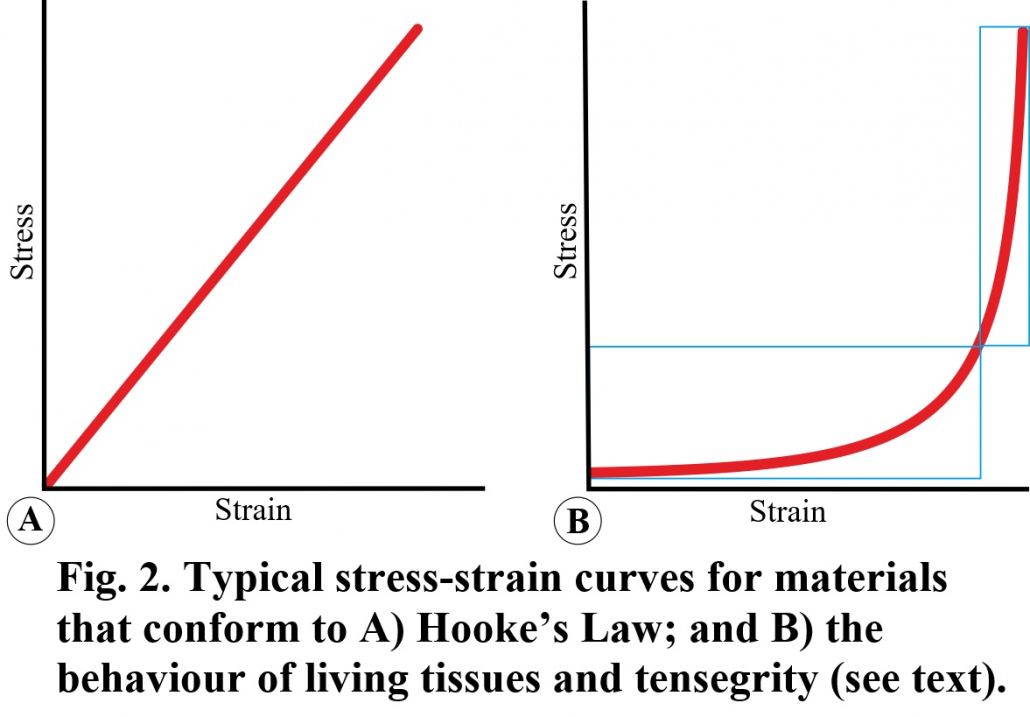
Current biomechanical theory is largely founded on the laws of classical mechanics as formulated by Galilei, Newton and Hooke, etc., but these ‘rules’ were based on the behaviour of inanimate objects and do not necessarily apply to the nonlinear dynamics of living tissues (Levin and Lowell de Solórzano, 2024). Hooke’s Law, for example, describes the linear relationship between stress and strain with Young’s Modulus defining the slope of the curve, but this creates a problem when applied to biology. Living systems typically display a non-linear stress/strain relationship, but because this complicates the analysis, the tissues are generally considered to function within the more ‘vertical’ high stress/strain region and which is assumed to be a straight-line (Figure 2). Living tissues, however, tend to operate within the more ‘horizontal’ low stress/strain region, where they will be more responsive, consume less energy and operate more efficiently — all defining characteristics of living systems. As Harris noted: “to regard Young’s Modulus as a constant… is a very big simplifying assumption” because it will be different at each point along the non-linear curve (Harris, 2018).
Compressed joints
In addition, a characteristic of lever systems is that they generate compressive forces between their joint surfaces, yet the thickness of articular cartilage tends to reduce in larger (heavier) vertebrates (Malda et al., 2013), while a clear ‘space’ has been demonstrated in the human knee (femur-tibia) (Terayama et al., 1980; Levin and Madden, 2005; Hakkak et al., 2015) and elbow (humerus-radius) (Kim et al., 2002) in vivo, even when the bones are pushed together. The ability of cartilage to sustain high compressive loads in the knee and temporo-mandibular (jaw) joints has also been questioned (Andrews, Shrive and Ronsky, 2011; Kim et al., 2012; Juran et al, 2013), while a review of the literature on temporo-mandibular mechanics noted a conspicuous lack of in vivo information available to support the lever model (Scarr and Harrison, 2016). To put it bluntly, biomechanics does not have a satisfactory model to explain how synovial joint surfaces could be routinely decompressed, or even ‘pulled apart’, and it is considered that this inadequacy has severely restricted our understanding of normal function.
Transient stress concentrations
“A lever system cannot passively stabilize itself in the presence of unexpected forces and moments, and the assignment of this role to the action of responsive muscles only transfers this latency elsewhere, and ultimately to an external neural controller that is presumed capable of providing the necessary ‘catch-up’ stability. However, even the fastest mono-synaptic reflex experiences a time-delay (Del Vecchio, 2023) which means that the necessary timing and precision required to neutralize the effects of sudden perturbations in the system is open to compromise (Cabe, 2019; Fultot et al., 2019). An abrupt change in force dynamics could create transient peak stress concentrations before the system has had time to react (Lin et al., 2019), and although engineered structures can be heavily reinforced against the potentially damaging effects of these (Salvadori, 2002) p. 84), it is likely that this inherent vulnerability would adversely affect living tissues (Levin, 2015).”
“Traditional musculoskeletal analysis has tended to focus on steady-state forces and kinematics and paid little attention to transients, but the transient properties of force generation are immensely important (Lin et al., 2019; Hayati et al., 2020). Until recently, the rate of change of force over time had no standard term in physics, and as a result, the dynamics of force transients have been simplified through the same analytic methods and formalisms as used in engineering (Freutel et al., 2014; Deriglazov, 2017)” (Scarr et al., 2024).
“Here, the concepts of force, velocity, momentum, torque and acceleration, etc., are typically processed through 1st and 2nd order differential equations without the need to account for their higher-order (3rd, 4th…) derivatives, but the assumption that this approximation is also valid for living tissues is not necessarily the case. Put simply, a force impact is not an instantaneous event but a transient one: a derivative of momentum that rapidly escalates and takes time to reach its peak (Figure 3). The transient after acceleration is jerk and followed by snap and crackle, respectively (He et al., 2015; Eager et al., 2016). The 1st derivative of force over time — yank — is then highly significant because it is proportional to jerk (Lin et al., 2019), and an unexpected force impact that generates peak stress concentrations faster than the tissues can react to carries the potential for injury at relatively low speeds and forces.” (Scarr et al., 2024).

The effects of these mechanical transients coupled with the long healing times required for post-traumatic recovery, then suggest that such peak loadings and intractable instabilities (inherent in the lever model) would lead to material fatigue and destructive tissue failure, which further highlights the problem with orthodox biomechanical thinking (Scarr et al., 2024). However, before examining the advantages of tensegrity mechanics to living systems, it is appropriate to introduce some of the key players involved.
4. The origins of biotensegrity
R. Buckminster Fuller
As a maverick thinker and inventor, Fuller (1895-1983) had been developing a system of geometry based on first principles since the 1920’s, and not satisfied with conventional explanations that used the cube with its 90o angles as the frame of reference, considered that a coordinate system based on 60o was far more fundamental, and developed his theory of Synergetics as ‘the study of nature’s coordinate system’ (Fuller, 1982; Edmondson, 2007). Fuller perceived that all natural forms were the result of matter being acted upon by invisible forces and proposed them as finite energy systems consisting of tension and compression acting together. He also recognized the sphere as the ultimate compression element — because it resists external forces equally from every direction — and focused on a shape that mimics it structurally: the icosahedron with its twenty triangular faces that can be subdivided and form higher-order icosahedra that come ever closer to approximating the sphere. Fuller is thus best known for his geodesic domes (Krause and Lichtenstein, 1999), but it is the icosahedral symmetry that is most significant here.
The geometry of the geodesic dome was the inspiration that resolved the outer structure of the spherical viruses and fullerene molecule C60 (Caspar, 1980; Kroto, 1990), and also appears in radiolaria, pollen grains and clathrin vesicles. Fuller also recognized the bicycle wheel as a tensegrity structure with the compressed hub and outer rim held both apart and together by the tensioned spokes — and which maintain the wheel’s integrity — and the mechanics of the shoulder (Levin, 1997), pelvis (Levin, 2007) and temporo-mandibular joints (Scarr and Harrison, 2017) have all been compared with the bicycle wheel. Fuller was thus using his new method of geometry to demonstrate a dynamic architecture based on nature’s principles and began spreading the word
Kenneth Snelson
As a young art student attending Fuller’s lectures in 1948, Kenneth Snelson (1927-2016) was so impressed that he returned the following year with his own sculpture (the X-Piece) constructed from pieces of wood that were suspended — or appeared to float — within a tensioned network of nylon cables (Snelson, 1996), and Fuller immediately recognized its significance. “Simple as this pioneering work was, it pointed ahead to the possibility of structures in which form and function truly are… one, and the visible configuration of the sculpture is simply the revelation of otherwise invisible forces” (Heartney, 2009) p. 20); and this statement is the key to appreciating tensegrity in a biological context: the physical representation of invisible forces.
Both Fuller and Snelson contributed to the development of tensegrity but ultimately went their separate ways. By the 1970’s, Fuller was becoming a household name with his geodesic domes springing up all over the place (Krause and Lichtenstein, 1999), but he always maintained that tensegrity was really a design principle of nature (Fuller, 1982). Snelson successfully pursued a career in sculpture but remain convinced that tensegrity had no real value except in art (Snelson, 1996), yet the irony of this is that his sculptures have been the inspiration to others in exploring tensegrity in a biological context.
Donald E. Ingber
As an undergraduate student in 1975, Ingber recognized similarities between a tensegrity model and the behaviour of cells when compressed — with both springing back to their original shape when released — a finding that later inspired his research as a cell biologist and work on the architecture of cancerous tissues (Ingber, 2023). Since then, Ingber’s work has provided much of the empirical support for tensegrity in integrating the mechanics of the cellular cytoskeleton and extracellular environment with internal chemical signalling cascades, changes in cell function and the development of complex organs and tissues (Ingber et al., 2014).
Stephen M. Levin
As an orthopaedic surgeon in the 1970’s, Levin noted things at the operating table that could not be explained by conventional mechanical theory and began searching for more plausible explanations by examining the skeletons of dinosaurs and other animals (Levin, 2002; 2015). Dinosaurs are essentially no different from any other vertebrate except that they could weigh up to 100 tons (Mitchell and Sander, 2014), and as a doubling in height implies a cubic increase in volume and mass, Levin wondered how the immense weight of these creatures could be supported and moved through a lever system that would have placed enormous stresses on their tissues, especially as the neck and tail can extend up to 10 metres from their bodies.
He also noticed that while most engineered structures transfer their weight to the ground through continuous compression, the struts within Snelson’s tensegrity structures are suspended within the tensioned network of cables and form a truss system that distributes mechanical stresses through the system in a way that remains completely stable, irrespective of the direction of gravity. Snelson’s sculptures then stimulated the idea that tensegrity might provide a viable alternative to traditional biomechanical explanations because it can be applied at every structural level within a complex heterarchy and avoids potentially damaging stress concentrations (Levin, 1982; 2002; 2015) During development, tension and compressional forces would interact in ways that lead to the formation of complex tissues and conform to a fundamental set of self-organizing principles.
5. Principles of self-organization
At the most basic level, atoms interact with each other in a number of different ways — van der Waal’s forces, electrostatics, hydrogen bonding, covalency and steric-repulsion etc. — all of which can be categorized into those that ‘pull’ atoms together and others that keep their centres apart. Of course, there is a lot more detail associated with these processes, but simplifying then into this duality of attraction and repulsion reveals them to be the drivers that cause atoms to spontaneously organize themselves into the most stable and energy-efficient configurations as mineral crystals and more flexible molecules (Levin, 2015; Scarr, 2018).
Such arrangements form as they do because of some fundamental principles of self-organization: geodesic geometry, close-packing and the minimization of energy — and which apply at every size-scale — where attraction and repulsion at higher size-scales are now referred to as tension and compression and can be modelled through tensegrity. Crystals and molecules then become close-packed tensegrity configurations of atoms with invisible struts (Edwards et al., 2012; Bywater, 2017; Reilly and Ingber, 2018; Eichenauer and Lordick, 2019).
Tensegrity frameworks are inherently geodesics because their structural members transfer tension and compressional forces along the shortest pathways and in straight lines. They are close-packed because their component parts automatically get as close as they can to each other, and they always settle into a state of minimal-energy. The tension elements pull the nodes together, and the compression elements keep them apart, with the tensegrity framework being the embodiment of these three basic principles and the physical representation of the invisible forces within it. The intrinsic tension (self-stress) contained in both living tissues and tensegrity models also means that the initial part of the stress-strain curve never reaches zero stress and that they are always ‘primed for action’ (Masi and Hannon, 2009) (Figure 1B).
So, rather than thinking of the human body in terms of separate ‘bits’, like a machine, a biotensegrity perspective considers their relationships within a complex heterarchical system and examines each ‘part’ in relation to the whole (Levin, 2015; Scarr, 2018). We might then think that tensegrity represents the way forward in biomechanics, but there is a potential problem with this word in a biological context because of the way it has been applied in mechanical engineering.
Tensegrity or biotensegrity
Both Fuller (1982) and Snelson (Snelson, 1996) emphasized that the compression members within a tensegrity framework remain distinct — “continuous tension and discontinuous compression” — while (Skelton et al., 2001) relaxed this requirement and defined a class-k tensegrity structure as “a stable equilibrium of axially-loaded elements with a maximum of k compressive members connected at the node”. Here, a node (joint) can include any number of compression members with just one defining class k-1, two defining class k-2, and so on, which means that Fuller and Snelson’s definition only apply to class k-1. So, while this classification is useful in an engineering context, the observations that living bones are not heavily compressed — and can even maintain a space between their articular surfaces (Terayama, Takei and Nakada, 1980; Levin and Madden, 2005; Andrews et al., 2011; Hakkak et al., 2015) — implies that Skelton et al (2001) definition is not applicable to living systems, and as a consequence, Levin introduced the term biotensegrity in order to make this distinction clear (Levin, 2002).
Of course, both fields are closely linked and can benefit from each other, but while the term tensegrity refers to the mechano-structural principle, the concept of biotensegrity relates more to the invisible force vectors and dynamic complexity of the system, i.e. “a world of processes rather than a world of things” (Dupre and Nicholson, 2018). So, although most of the bio-focused literature has used the word tensegrity out of tradition (Turvey and Fonseca, 2014; Boghdady et al., 2021; Ingber, 2023), it should be noted that the two terms are not necessarily synonymous. Living organisms are relatively light, flexible and capable of functioning much the same in any position, and because they have refined themselves over hundreds of millions of years of evolution, it is likely that they have already found the most energy-efficient ways of doing things.
6. The mechanics of life
Closed-chain kinematics
Closed kinematic chains (CKCs), or linkage systems, have long been employed in mechanical engineering because they provide a simple and efficient mechanism with multiple applications. Here, multiple bars are coupled into continuous mechanical loops with each one influencing the position, motion, and stability of all the others and enabling the controlled transfer and amplification (or attenuation) of force, speed and kinetic energy (Figure 4). CKCs have also been described in the feeding mechanisms of fish (Muller, 1996; Farina et al., 2019), shrimps and reptiles; and the jaws and limbs of humans (Valero-Cuevas et al., 2007; Levin et al., 2017; Scarr and Harrison, 2017; Olsen, 2019; Burgess, 2021).
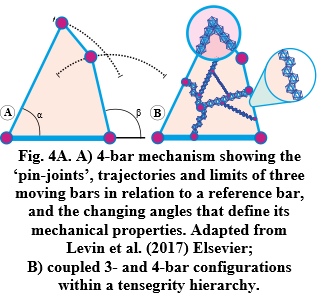
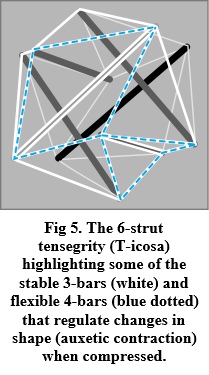
Kinematics is all about the geometry of motion and generally described through algebraic equations, yet a graphic portrayal of their geometries reveals things that might otherwise not be appreciated, and which are particularly relevant here because closed-chain kinematics constitutes the basic mechanics of tensegrity (Figure 5). The 4-bar mechanism is then highlighted because it enables the structure itself to control the position and motion of every part of the system — from molecules to the complete organism — with the 3-bars creating the stability that allows the 4-bars to change shape, while those with five or more bars are uncontrollable on their own but can be part of more complex systems (Rimoli and Pal, 2017).
The controlled transfer of power
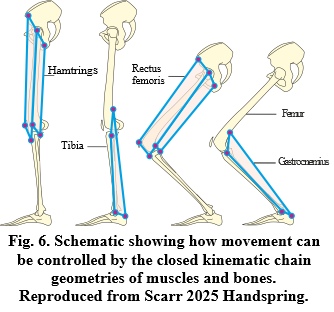
Of course, these CKCs might just appear to be complex lever systems, but this is not the case from a bio-perspective where each anatomical ‘bar’ (cable or strut) and ‘node/pin-joint’ consists of multiple sub-structures organized in the same way within a vast global heterarchy that extends down to the molecular level (Reilly and Ingber, 2018) (Figure 4B). Here, each bar is under tension or compression and mechanically integrated with all the others at every level, so that when one part changes in length or position the entire system becomes involved. Mono-articular muscles might then be considered as variable-length bars within 3-bar systems, while bi-articular muscles can form tensionally stiff bars within 4-bar systems that enable multiple joints to be coupled together, and in ways that enable power to be transferred from one part of the body to another in a controlled way (Levin et al., 2017; Dischiavi et al., 2018) (Figure 6).
Such closed-chain systems are then significant because they enable motion to be controlled from within the structure itself and in ways that are beyond the sole capability of the nervous system (Valero-Cuevas et al., 2007; Saxena et al., 2012). They also enable the tissues to respond instantly to rapidly changing conditions and operate much faster than muscles can contract — thus overcoming the problems with the lever model, force transients and potentially-damaging stress concentrations (Scarr et al., 2024) — thus allowing muscle generated forces to be transmitted over a much wider field than is generally appreciated (Dischiavi et al., 2018; Levin and Scarr, 2022) with degeneracy built into the complexity of the system (Wilson and Kiely, 2016).
Evolutionary implications
Muller (Muller, 1996) reviewed the mechanics of the 4-bar mechanism in animals and highlighted two important features. First, that changes in shape map non-linearly to the kinematic transmission ratio (KT) — an emergent property that also characterizes the behaviour of living tissues (Section 3); and second, that changes in the relative lengths of the bars leads to a redundant many-to-one mapping (MTOM), where different 4-bar shapes can produce the same mechanical output (KT), and with evolutionary implications because it permits a partial decoupling between morphological diversity and function. In other words, it explains how one part of the anatomical CKC/tensegrity system could change in shape — whilst keeping the same mechanical function — within a global collective of gradual step-by-step processes that ultimately leads to the transition of one species into another (Alfaro et al., 2005; Muñoz, 2019). It is also likely that such MTOM is involved in embryological development, as each anatomical ‘part’ gradually evolves in shape, position and function in response to the mechanics of its local environment, changes in cellular behaviour (Ingber, 2023) and those basic principles of self-organization (Section 5).
Living organisms are thus not static but in a constant state of flux (Pascal and Pross, 2015; Nicholson, 2018), and all the examples in this chapter are snapshots of systems that are constantly changing. The planar 4-bar is then highlighted because of its mechanical simplicity and as the first iteration of the omni-directional CKC/tensegrity heterarchy (Figures 4 & 5), with the behaviour of each part dependent on both its internal structures and the wider environment (Turvey and Fonseca, 2014; Cabe, 2019), and the system as a whole controlling the flow of kinetic energy (Bejan, 2016). It should also be noted that the T-icosa model (Figures 1 & 5) contracts auxetically when compressed, and such a characteristic that increases density/pressure within the structure has been described in the heart, bladder (Levin, 2002), tendons (Gatt et al., 2015) and other soft-tissues (Ziauddin and Ali, 2013). The distinctive mechanical behaviours of biological tissues then makes a case for a distinction to be made between different types of model.
7. Classifying biomechanical models
(Humphrey, 2003) stated that: “the overall goal of biomechanics is… the general improvement of the human condition” — and which is a noble cause that no-one would wish to deny — but differences between the models used to fulfill that goal are often poorly appreciated. “While medical and social needs drive the enormous amount of research that takes place at every level, the employment of reductionism and engineering methodologies as a way of facilitating its goals has not been entirely consistent with the unbiased progression of anatomical knowledge (Dischiavi et al., 2018; Nicholson, 2019). Indeed, the ability to overlook the assumptions, approximations and unknowns inherent within its methods is routinely accepted as part of the modelling process, with such matters considered as minor inconveniences that can be safely ignored or re-examined following the acquisition of more data” (Scarr et al., 2024). And with this in mind, a new classification of biomechanical models that places them in a functional context is now introduced.
Class 1: The observable (fundamentally indeterminate) reality of living systems (Glazier and Davids, 2009).
Class 2: Interpretations of biology that support a particular hypothesis or viewpoint and appear to emulate Class 1, e.g. most bio-research (includes levers and CKC models).
Class 3: Engineered solution-oriented mechanisms that fill some medical or social need but clearly differ from Class 1, e.g. prosthetics, robotics and biomimicry.
Class 4: Engineered structures inspired by Class 1 but do not pretend to represent biology, e.g. machines and architecture (Gomez-Jauregui et al., 2023).
Sub-classes of 3 & 4: Engineered structures with relevance to class 2 modelling from a biotensegrity perspective, e.g. geodesic dome refs, bicycle wheel refs and Snelson’s sculptures (Snelson, 1996; Heartney, 2009).
Here, the accurate modelling of living systems (Class 1) must be considered aspirational because Class 2 interpretations of reality are always likely to be incomplete (although biotensegrity now presents a conceptual modelling framework (see Section 10)). Class 2 models fill the contents of most bio-oriented textbooks and research papers — and are essential to the progress of human knowledge — but can become established within a tradition that erroneously accepts them as accurate representations of reality (e.g. levers, machines). Classes 3 and 4 are then substantially different from Class 1, although can be greatly influenced by it, because they are oriented towards practical solutions and can use whatever means necessary to achieving this. Unfortunately, many of the simplifying assumptions that are legitimately made in Classes 3 and 4 have been incorporated into Class 2 models with embedded historical dogmas, outdated methodologies and the best of intentions creating a subjective bias simply because there has been no viable alternative until recently (Levin and Lowell de Solórzano, 2024; Scarr et al., 2024).
Of course, there is a fair amount of overlap between these classes, and which are presented more as ‘food for thought’ with the distinctions between them being most significant. Classes 3 and 4 are largely constrained by the properties of the materials used, practicality of construction and cost, while living systems (Class 1) are constrained only by those fundamental principles.
Class 2 tensegrity models have been described in relation to molecules (Edwards et al., 2012; Bywater, 2017; Reilly and Ingber, 2018; Azulay et al., 2022), viruses (Sitharam and Agbandje-Mckenna, 2006), spider silk (Fraternali et al., 2020), cells (Ingber et al., 2014; Fraldi et al., 2019), tissues (Boghdady et al., 2021; Ingber, 2023) and regional anatomy, including the cranial vault (Scarr, 2008), temporo-mandibular joint (Scarr and Harrison, 2017), spine (Levin, 2002), shoulder (Levin, 1997), elbow (Scarr, 2012), pelvis (Levin, 2007; Pardehshenas et al., 2014), knee (Kim and Turvey, 2018), foot (Kiely and Collins, 2016; Wilson and Kiely, 2016), heart (Parker and Ingber, 2007), avian lung (Maina, 2017), human lung (Ingber, 2023), brain (Van Essen, 2023), postural control (Cabe, 2019; Doyon et al., 2019; Mangalam et al., 2020), homeostasis (Stamenović and Smith, 2020b) and the body as a whole (Levin, 2015; Dischiavi et al., 2018; Scarr, 2018; Levin and Lowell de Solórzano, 2024).
Class 2/3 models of the spine (Melnyk and Pitti, 2018; Oh et al., 2022) and limbs (Jung et al., 2021; Brandão and Savi, 2022; Abourachid et al., 2023) have also been developed in relation to prosthetics and robotics, but It is important to note that Class 2 tensegrity models cannot be meaningfully assessed from an engineering (Class 3/4) perspective (Gomez-Jauregui et al., 2023) without considering their biological (Class 1) complexities.
The role of tensegrity has also been described in plant physiology (Mirabet et al., 2011; Witztum and Wayne, 2014), and recognized within cancer research (Dinicola et al., 2011; Tadeo et al., 2014), clinical decision-making (Fullerton, 2018; Crowle and Harley, 2020; Scarr, 2020), social systems (Primus, 2022) and team sports (Caldeira et al., 2020), illustrating the scope of this relatively new systems-biology modelling approach. Understanding the benefits of a biotensegrity perspective to biomechanical modelling, prosthetics, robotics and mechanical engineering in general thus means starting at the beginning.
8. A new type of physical law
The Italian Renaissance witnessed a dramatic increase in knowledge that now forms the basis for modern scientific thinking, but there is a problem. The reductive methods of science have tended to concentrate their efforts on the genetic code, molecular pathways and structural analysis, and largely ignored the simplicity of those fundamental rules of self-organization because they are ‘just too simple’ (Section 5). So, while Fuller’s theory of Synergetics as the study of nature’s coordinate system can seem rather cryptic and should not be taken as explicitly scientific, it contains ideas that are revolutionary in their scope and depth (Fuller, 1982; Edmondson, 2007).
Platonic ‘solids’
Geometric patterns and shapes do not just appear out of nowhere but because of some basic physical rules (Edmondson, 2007; Bejan, 2016), and Fuller recognized the significance of the Platonic ‘solids’ as a set of regular shapes that emerge from a sphere: the centrepiece of his universal system of geometry (Figure 7). Here, their edges can be projected onto the surface of a sphere and divide it into faces of equal size, while multiple spheres can close-pack into hexagonal arrangements in 2-D and the Platonic shapes in 3-D (Eichenauer and Lordick, 2019).
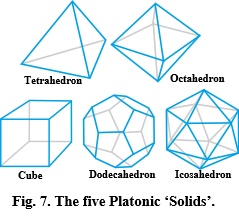
Bubbles and foams
Bubbles naturally form spheres because the pressures acting on their surfaces are balanced in every direction, but true spheres don’t exist in the real world because they are just mathematical constructs. Soap bubbles may look like spheres but have surfaces that consist of lots of irregularly shaped molecules that maintain the overall shape through surface tension; and Fuller appreciated that while a high-order icosahedron closely approximates the space-filling efficiency of the sphere, this can be represented by the T-icosa model as the omnidirectional balance of tension and compression (Figure 1), and archetypal model for biology.
Bubbles naturally follow Plateau’s Laws and spontaneously organize into arrays that minimize the overall surface area, with bubble surfaces always meeting in groups of three, and edges that always intersect in fours at the tetrahedral angle of 109.47o (Serón et al., 2022). Similar-size bubbles automatically form hexagonal arrangements, and this pattern also appears in the close-packing of actin and myosin molecules within muscles (Standring, 2005) p. 118), parabronchi within the avian lung (Maina, 2017), eyes of insects and honeycomb of the bee, etc. (Thompson, 1917). Living cells frequently close-pack into hexagonal patterns but are not constrained solely by Plateau’s Laws because of the higher levels of complexity (Graner and Riveline, 2017). The tetrahedral angle also appears at the junctional offset between hexagonal cells on either side of the bee’s honeycomb, and closely matches the angular connections between trabeculae within bone (Reznikov et al., 2016).
Helices and crossed-helical tubes
The tetrahedron is then further interesting because it can close-pack with others to form a tetrahelix (Boerdijk–Coxeter helix) (Lord and Ranganathan, 2001) as the geometric basis for molecular helices (Sadoc and Rivier, 2000; Lord, 2002), with the helix being a common motif in protein structures and a general model for coiled winding in a wide variety of different organisms and tissues at many different levels (Scarr, 2016; Fratzl et al., 2022); and ultimately, crossed-helical arrangements of collagen fibres that reinforce the tubular walls of arteries, muscles, gastrointestinal tract and intervertebral discs and mechanically control changes in their shape (Shadwick, 2008; Scarr, 2016). In addition, the faces of the pentagonal dodecahedron give rise to the Golden Ratio, Fibonacci Sequence and helical/spiral configurations in plants (Rivier et al., 2016), cephalopods, mammals (Scarr, 2016) and humans (Persaud-Sharma and O’Leary, 2015).
The geometries of the Platonic ‘solids’ have thus been linked with the close-packing efficiencies of spheres (icosahedron) and helices/spirals (tetrahedron/dodecahedron), and directly relate to those basic principles of self-organization and tensegrity (Section 5), with (bubble) foams being the simplest examples of soft-matter physics (Drenckhan et al., 2005; Rivier et al., 2016) that also includes the complex behaviours of polymers (molecular helices), colloids, surfactants and liquid crystals within living systems (Hirst, 2013; van der Gucht, 2018). Simplicity and complexity are thus more closely related than is often appreciated with all the above now considered relevant to addressing Schrodinger’s (1944) suggestion for “a new type of physical law”, and the concept of biotensegrity changing traditional thinking about structure and the mechanics of life.
9. Updating anatomy
The notion that the musculo-skeletal duality constitutes the basic structural framework of the body is now well-established but was conceptually rivalled in the 18th century by a system of connective tissue compartments that (Lamarck, 1963) p. 230) declared to be “…the universal matrix of all organization”, but which gradually faded in significance as the ‘muscles moving bones/lever paradigm’ assumed functional dominance (Scarr et al., 2024) (Section 3). As a consequence, the fascial tissues have been widely dismissed as mere packing tissue or relegated to ancillary roles but are now recognized for their involvement in structural stability, motion control and the aetiology of cancers and other pathologies (Dischiavi et al., 2018; Wilke et al., 2018).
The term fascia refers to the soft collagen-rich connective tissues that form a complex fibrous/fluid (soft-matter) network that surrounds virtually every cell in the body as the extracellular matrix (ECM) (Mao and Wickstrom, 2024) and is continuous with the tougher fibrous sheaths that enclose and permeate every organ, muscle and tissue, so that at the microscopic scale there is no clear distinction between where one part ends and another begins (Guimberteau et al., 2010; Guimberteau and Armstrong, 2015).
A reassessment of those forgotten tissue compartments from a biotensegrity perspective recently considered the fascial system as a globally-tensioned fibrous network encompassing a complex heterarchy of regionally specialized compartments under compression (i.e. tensegrity), and concluded that this intrinsically stable functional entity constitutes the basic structural/architectural framework of the human body (Scarr et al., 2024). Here, muscles and bones are no-longer separate entities but compartmental specializations of the global fascial system, and which together with the underlying mechanics of CKC/tensegrity suggests that the fascial system should now be considered as the primary controller of movement and acts in synergy with the nervous system (where befits) (Cabe, 2019; Fultot et al., 2019), and which effectively renders the term musculo-skeletal obsolete.
The intimate relationship between the cytoskeleton and ECM is then particularly significant because it mechanically couples the latter with internal chemical signalling cascades and changes in cell function (Boghdady et al., 2021; Ingber, 2023), and influences the formation and behaviour of the fascial system and body as a whole through the mechanics of CKC/tensegrity.
10. Stability before Movement
Until recently, biomechanics has tended to focus on movement, with muscles and bones taking centre stage and the nervous system providing the necessary catch-up stability for transient muscular latencies, and some of the problems with this were described in Section 3. The reassessment of the fascial system as an intrinsically-stable architecture of tensioned fibrous tissues and compressed compartments then offers an alternative approach (through biotensegrity), but an issue now arises with the word stability because it evokes images of firmness, fixity and permanency, while stability in dynamic systems is inseparable from its opposite: change (Pascal and Pross, 2015; Bejan, 2016). Textbook descriptions of anatomy can give impressions of unchanging stability but are really just Class 2 snapshots of dynamic systems that are constantly changing.
Super-stability
So, if this intrinsically stable framework is constantly changing, there must be some sort of homeostatic algorithm that keeps all its internal processes orderly, but until recently, there has been no ready-made math for determining whether such a framework really is intrinsically stable, which is why biomechanics has been dominated by heuristic approaches that can at least provide partial solutions (Freutel et al., 2014). (Connelly and Back, 1998), however compared the spider web with the mathematics of tensegrity and highlighted the algorithmic framework of super-stability — a fundamental theorem that now formalizes biotensegrity as a viable model for living systems (Figure 8).
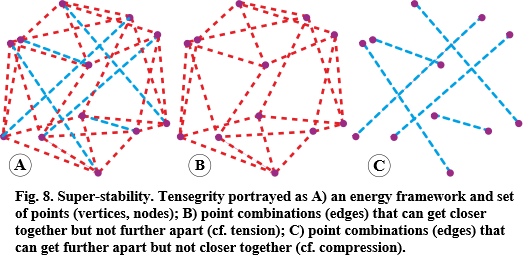
Super-stability encompasses the tensegrity variables of tension and compression and has relevance to living systems because they conform to the same self-organizing principles (Wertheim, 2006). Here a system is mathematically represented as a set of points (vertices, nodes) connected by edges with simple distance constraints, with certain combinations that can get closer to each other but not further apart, and others that can get further apart but not closer together. The edges are thus representing tension and compression springs that can change in length and vary the amount of stored elastic-energy (Yang et al., 2019; Connelly and Guest, 2022).
The stability of the system is then achieved through coupled changes in the elastic strain energies as the springs automatically seek their minimal states, and because these energy functions are split between positive (tension) and negative (compression), such a system will always resolve itself into the most stable and energy-efficient configuration at any given moment in time; but as a super-stable framework, it can have ANY number of possible edge combinations for ANY number of vertices and without restricting the assignments.
Here, the edges can be freely split into shorter ones with new vertices, thus increasing their total count within the framework, or connected into longer ones that decrease the number of vertices, and all without compromising the system’s stability. In other words, the edges can get longer, shorter, divide, merge or even switch energy functions with the entire system involved in making these transitions, and the configuration as a whole remaining completely stable throughout — no matter how complicated it becomes — and the value of this as a representation of dynamic anatomy cannot be overstated.
At the highest, most abstract level, super-stable tensegrity provides the intrinsic-stability solution for ANY comparable framework of edges and vertices, regardless of the number of elements within it, and it does so through the minimal-energy principle. Super-stability is essentially a representation of infinity, and the imagery of such a framework that can freely switch between an infinite number of different combinations of edges and vertices then allows a shift to be made from the virtual, abstract and logical perspective to the more tangible morphological transformations of biology and its processes (Dupre and Nicholson, 2018). Here, the local, regional and global meta-stabilities of attraction/repulsion and tension/compression are constantly re-organizing themselves in response to the ever-changing environment, and enabling each ‘part’ to grow, multiply, transform, repair and move with the system as a whole maintaining its stability.
In other words, a complex multi-level framework that is constantly changing and maintaining the viability of the system through its myriad interconnected processes, and which then places super-stable tensegrity as the ultimate Class 2 biomechanical model, and biotensegrity as the super-stability hypothesis for biology.
Bibliography
Abourachid, A., Chevallereau, C., Pelletan, I., and Wenger, P. (2023). An upright life, the postural stability of birds: a tensegrity system. Journal of the Royal Society Interface, 20:20230433.
Alfaro, M.E., Bolnick, D.I., and Wainwright, P.C. (2005). Evolutionary consequences of many-to-one mapping of jaw morphology to mechanics in labrid fishes. The American Naturalist, 165:140-154.
Andrews, S., Shrive, N., and Ronsky, J. (2011). The shocking truth about meniscus. Journal of Biomechanics, 341:34-55.
Azulay, H., Lutaty, A., and Qvit, N. (2022). How similar are proteins and origami? Biomolecules, 12:622.
Bejan, A. (2016). Life and evolution as physics. Communicative and Integrative Biology, 9: e1172159.
Boghdady, C.M., Kalashnikov, N., Mok, S., McCaffrey, L., and Moraes, C. (2021). Revisiting tissue tensegrity: Biomaterial-based approaches to measure forces across length scales. APL Bioengineering, 5:041501.
Borelli, G. (1680). De moto animalium. Lugduni batavorum: Petrum Vander Aa.
Brandão, A., and Savi, M.A. (2022). Nonlinear mechanics of a smart biotensegrity human foot Prosthesis. International Journal of Applied Mechanics, 14:2150124.
Burgess, S. (2021). A review of linkage mechanisms in animal joints and related bioinspired designs. Bioinspiration and Biomimetics, 16:041001.
Bywater, R.P. (2017). A tensegrity model for hydrogen bond networks in proteins. Heliyon, 3:e00307.
Cabe, P.A. (2019). All perception engages the tensegrity-based haptic medium. Ecological Psychology, 31:1–13.
Caldeira, P., Fonseca, S.T., Paulo, A., Infante, J., and Araújo, D. (2020). Linking tensegrity to sports team collective behaviors: towards the group-tensegrity hypothesis. Sports Medicine, 6:24.
Caspar, D.L.D. (1980). Movement and self-control in protein assemblies. Quasi- equivalence revisited. Biophysics Journal, 32:103–138.
Connelly, R., and Back, A. (1998). Mathematics and tensegrity. American Scientist, 86:142-151.
Connelly, R., and Guest, S.D. (2022). Frameworks, tensegrities, and symmetry. Cambridge: Cambridge University Press.
Crowle, A., and Harley, C. (2020). Development of a biotensegrity focused therapy for the treatment of pelvic organ prolapse: A retrospective case series. Journal of Bodywork and Movement Therapies, 24:115–125.
Del Vecchio, A. (2023). Neuromechanics of the rate of force development. Exercise and Sport Sciences Reviews, 51:34–42.
Deriglazov, A. (2017). Classical mechanics: Hamiltonian and Lagrangian formalism. 2nd ed. Springer Nature.
Dinicola, S., D’Anselmi, F., Pasqualato, A., Proietti, S., Lisi, E., Cucina, A., and Bizzarri, M. (2011). A systems biology approach to cancer: fractals, attractors,
and nonlinear dynamics. OMICS A Journal of Integrative Biology, 15:93–104.
Dischiavi, S.L., Wright, A.A., Hegedus, E.J., and Bleakley, C.M. (2018). Biotensegrity and myofascial chains: A global approach to an integrated kinetic chain. Medical Hypotheses, 110:90–96.
Doyon, J.K., Hajnal, A., Surber, T., Clark, J.D., and Kelty-Stephen, D.G. (2019). Multifractality of posture modulates multisensory perception of stand-on-ability. PLoS ONE, 14:e0212220.
Drenckhan, W., Hutzler, S., and Weaire, D. (2005). Foam physics: The simplest example of soft condensed matter. In: AIP Conference Proceedings. 22–28.
Dupre, J., and Nicholson, D.J. (2018). A manifesto for a processual philosophy ofbiology. In: D. Nicholson and J. Dupre, eds. Everything flows: towards a processual philosophy of biology. Oxford: Oxford University Press. pp.3–45.
Eager, D., Pendrill, A.M., and Reistad, N. (2016). Beyond velocity and acceleration: Jerk, snap and higher derivatives. European Journal of Physics, 37:065008.
Edmondson, A.C. (2007). A Fuller explanation: the synergetic geometry of R. Buckminster Fuller. Colorado: Emergent World Press.
Edwards, S.A., Wagner, J., and Gräter, F. (2012). Dynamic prestress in a globular protein. PLoS Computational Biology, 8:1002509.
Eichenauer, M.F., and Lordick, D. (2019). How Platonic and Archimedean solids define natural equilibria of forces for tensegrity. FME Transactions, 47:234–244.
Ellers, Olaf., Ellers, Kai-Isaak., Johnson, A.S., Po, T., Heydari, S., Kanso, E., and McHenry, M.J. (2024). Soft skeletons transmit force with variable gearing. Journal of Experimental Biology. 227:246901.
Farina, S.C., Kane, E.A., and Hernandez, L.P. (2019). Multifunctional structures and multistructural functions: integration in the evolution of biomechanical systems. Integrative and Comparative Biology, 59:338–345.
Fraldi, M., Palumbo, S., Carotenuto, A.R., Cutolo, A., Deseri, L., and Pugno, N. (2019). Buckling soft tensegrities: fickle elasticity and configurational switching in living cells. Journal of the Mechanics and Physics of Solids, 124:299-324.
Fraternali, F., Stehling, N., Amendola, A., Anrango, B.A.T., Holland, C., and Rodenburg, C. (2020). Tensegrity modelling and the high toughness of spider dragline silk. Nanomaterials, 10:1–15.
Freutel, M., Schmidt, H., Dürselen, L., Ignatius, A., and Galbusera, F., (2014).
Finite element modeling of soft tissues: material models, tissue interaction and challenges. Clinical Biomechanics, 29:363–372.
Fuller, R.B. (1982). Synergetics: explorations in the geometry of thinking. New York: Collier Macmillan.
Fullerton, B.D. (2018). Biotensegrity: how ultrasound diagnostics guide regenerative orthopedic therapies to restore biomechanical function. In: I. Kohlstadt and K. Cintron, eds. Metabolic therapies in orthopedics, 2nd ed. Boca Raton: Taylor and Francis. pp.91–109.
Fultot, M., Frazier, P.A., Turvey, M.T., and Carello, C. (2019). What are nervous systems for? Ecological Psychology, 31:218–234.
Gatt, R., Wood, M., Gatt, A., Zarb, F., Formosa, C., Azzopardi, K., Casha, A., Agius, T., Schembri-Wismayer, P., Attard, L., and Al, E., (2015). Negative Poisson’s ratios in tendons: an unexpected mechanical response. Acta Biomaterialia, 24:201–208.
Glazier, P.S., and Davids, K. (2009). The problem of measurement indeterminacy in complex neurobiological movement systems. Journal of Biomechanics, 42:2694–2696.
Gómez-Jáuregui, V., Carillo-Rodriguez, A., Manchado, C., and Lastra-Gonzalez, P. (2023). Tensegrity applications to architecture, engineering and robotics: a review. Applied Sciences, 13:8669.
Graner, F., and Riveline, D., (2017). ‘The forms of tissues, or cell-aggregates’: van der Gucht, J. (2018). Grand challenges in soft matter physics. Frontiers in Physics, 6:87.
Guimberteau, J-C., Sawaya, E.T., and Armstrong, C. (2024). Intra-tissue endoscopic exploration under the skin of living patients: an invitation to re-think the nature of human living matter. Journal of Bone Research and Orthopaedic Surgery, 2:103.
Hakkak, F., Jabalameli, M., Rostami, M., and Parnianpour, M. (2015). The tibiofemoral joint gaps – an arthroscopic study. SDRP Journal of Biomedical Engineering, 1:1–6.
Harris, A.K. (2018). The need for a concept of shape homeostasis. BioSystems, 173:65–72.
Hayati, H., Eager, D., Pendrill, A.-M., and Alberg, H. (2020). Jerk within the context of science and engineering – a systematic review. Vibration, 3:371–409.
Heartney, E. (2009). Kenneth Snelson: forces made visible. Hard Press Editions.
Hirst, L. (2013). Fundamentals of soft matter science. Boca Raton: CRC Press.
Humphrey, J.D. (2003). Continuum biomechanics of soft biological tissues. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 459:3–46.
Ingber, D.E. (2023). From tensegrity to human organs-on-chips: implications for mechanobiology and mechanotherapeutics. Biochemical Journal, 480:243–257.
Ingber, D.E., Madri, J., and Jamieson, J. (1981). Role of basal lamina in neoplastic disorganization of tissue architecture. Proceedings of the National Academy of Sciences, 78:3901–3905.
Ingber, D.E., Wang, N., and Stamenović, D. (2014). Tensegrity, cellular biophysics, and the mechanics of living systems. Reports on progress in physics. Physical Society, 77:046603.
Jung, E., Ly, V., Cheney, C., Cessna, N., Ngo, M.L., and Castro, D. (2021). Design, construction and validation of a proof of concept flexible-rigid mechanism emulating human leg behavior. Applied Sciences, 11:9351.
Juran, C.M., Dolwick, M.F., and McFetridge, P.S. (2013). Shear mechanics of the TMJ disc: relationship to common clinical observations. Journal of dental research, 92:193–8.
Kiely, J., and Collins, D.J. (2016). Uniqueness of human running coordination: The integration of modern and ancient evolutionary innovations. Frontiers in Psychology, 7:262.
Kim, P.-T., Isogai, S., Murakami, G., Wada, T., Aoki, M., Yamashita, T., and Ishii, S. (2002). The lateral collateral ligament complex and related muscles act as a dynamic stabilizer as well as a static supporting structure at the elbow joint: an anatomical and experimental study. Okajimas Foka Anatomy Japan, 79:55–62.
Kim, W., Thambyah, A., and Broom, N. (2012). Does prior sustained compression make cartilage-on-bone more vulnerable to trauma? Clinical Biomechanics, 27:637–645.
Kim, W. and Turvey, M.T., 2018. The knee tensegrity system manages the balance between tension and compression. 6, 56–59.
Kirkby, R. (1975). The probable reality behind structural integration. Journal of Structural Integration.
Krause, J., and Lichtenstein, C., eds., (1999). Your private sky – R. BuckminsterFuller: the art of design science. Lars Müller.
Kroto, H. (1990). C60, fullerenes, giant fullerenes and soot. Pure and Applied Chemistry, 62:407–415.
Lamarck, J.B. (1963). Zoological philosophy: an exposition with regard to the natural history of animals. New York: Hafner.
Levin, S.M. (1981). The icosahedron as a biologic support system. 34th Annual conference Alliance for engineering in medicine & biology, 404.
Levin, S.M. (1982). Continuous tension, discontinuous compression. Bulletin of Structural Integration, 8.
Levin, S.M. (1997). Putting the shoulder to the wheel: a new biomechanical model for the shoulder girdle. Journal of Biomedical Sciences Instrumentation, 33:412–417.
Levin, S.M. (2002). The tensegrity-truss as a model for spine mechanics: biotensegrity. Journal of Mechanics in Medicine and Biology, 2:375–388.
Levin, S.M. (2007). A suspensory system for the sacrum in pelvic mechanics: biotensegrity. In: A. Vleeming, V. Mooney and R. Stoedkart, eds. Movement, stability and lumbopelvic pain, 2nd ed. Edinburgh: Elsevier.
Levin, S.M. (2015). Tensegrity: the new biomechanics. In: M. Hutson and A. Ward, eds. Oxford Textbook of Musculoskeletal Medicine, 2nd ed. Oxford University Press. 150–162.
Levin, S.M., and Madden, M.A. (2005). In vivo observation of articular surface contact in knee joints. Unpublished., Available at www.biotensegrity.com.
Levin, S.M., and Scarr, G. (2022). Biotensegrity and the mechanics of fascia. In: R. Schleip, P.A. Huijing, C. Stecco and M. Driscoll, eds. Fascia: the tensional network of the human body, 2nd ed. Edinburgh: Churchill Livingstone Elsevier.
Levin, S.M., and Lowell de Solórzano, S. (2024). Bouncing bones—ancient wisdom meets modern science in a new take on locomotion. Frontiers in Physiology, 15:1432410.
Levin, S.M. Lowell de Solórzano, S., and Scarr, G. (2017). The significance of closed kinematic chains to biological movement and dynamic stability. Journal of Bodywork and Movement Therapies, 21:664–672.
Lin, D.C., McGowan, C.P., Blum, K.P., and Ting, L.H. (2019). Yank: The time derivative of force is an important biomechanical variable in sensorimotor systems. Journal of Experimental Biology, 222:181414.
Lord, E.A. (2002). Helical structures: The geometry of protein helices and nanotubes. Structural Chemistry, 13:305–314.
Lord, E.A., and Ranganathan, S. (2001). Sphere packing, helices and the polytope {3, 3, 5}. European Physics Journal D, 15:335-343.
Maina, J.N. (2017). Pivotal debates and controversies on the structure and function of the avian respiratory system: setting the record straight. Biological Reviews, 92:1475–1504.
Malda, J., de Grauw, J.C., Benders, K.E.M., Kik, M.J.L., van de Lest, C.H.A., Creemers, L.B., Dhert, W.J.A., and van Weeren, P.R. (2013). Of mice, men and elephants: the relation between articular cartilage thickness and body mass. PLoS ONE, 8:e57683.
Mangalam, M., Chen, R., McHugh, T.R., Singh, T., and Kelty-Stephen, D.G. (2020). Bodywide fluctuations support manual exploration: Fractal fluctuations in posture predict perception of heaviness and length via effortful touch by the hand. Human Movement Science, 69:102543
Mao, Y., and Wickstrom, S.A. (2024). Mechanical state transitions in the regulation of tissue form and function. Nature Reviews Molecular Cell Biology. 25:654-670
Masi, A.T., and Hannon, J.C. (2009). Human resting muscle tone (HRMT): narrative introduction and modern concepts. Journal of Bodywork and Movement Therapies, 12:320–332.
Melnyk, A., and Pitti, A. (2018). Synergistic control of a multi-segments vertebral column robot based on tensegrity for postural balance. Advanced Robotics, 32:850–864.
Mirabet, V., Das, P., Boudaoud, A., and Hamant, O. (2011). The role of mechanical forces in plant morphogenesis. Annual Review of Plant Biology, 62:365–385.
Muller, M. (1996). A novel classification of planar four-bar linkages and its application to the mechanical analysis of animal systems. Philosophical transactions of the Royal Society of London. Series B, Biological sciences, 351:689–720.
Muñoz, M.M. (2019). The evolutionary dynamics of mechanically complex systems. Integrative and Comparative Biology, 59:705–715.
Nicholson, D.J. (2018). Reconceptualizing the organism: from complex machine
to flowing stream. In: D. Nicholson and J. Dupré, eds. Everything moves: towards a processual philosophy of biology. Oxford: Oxford University Press. 139–166.
Nicholson, D.J. (2019). Is the cell really a machine? Journal of Theoretical Biology, 477:108–126.
Oh, C.L., Keong, C.K., Nishimura, T., and Jae‐yeol, K. (2022). Multi‐directional shape change analysis of biotensegrity model mimicking human spine curvature. Applied Sciences, 12:2377.
Olsen, A.M. (2019). A mobility-based classification of closed kinematic chains in biomechanics and implications for motor control. Journal of Experimental Biology, 222:195735.
Pardehshenas, H., Maroufi, N., Sanjari, M.A., Parnianpour, M., and Levin, S.M. (2014). Lumbopelvic muscle activation patterns in three stances under graded loading conditions: proposing a tensegrity model for load transfer through the sacroiliac joints. Journal of Bodywork and Movement Therapies, 18:633–42.
Parker, K.K., and Ingber, D.E. (2007). Extracellular matrix, mechanotransduction and structural hierarchies in heart tissue engineering. Philosophical Transactions of the Royal Society B: Biological Sciences, 362:1267–1279.
Pascal, R., and Pross, A. (2015). Stability and its manifestation in the chemical and biological worlds. Chemical Communications, 51:16160–16165.
Persaud-Sharma, D., and O’Leary, J.P. (2015). Fibonacci series, Golden proportions, and the human biology. Austen Journal of Surgery, 2:1–6.
Piolanti, N., Polloni, S., Bonicoli, E., Giuntoli, M., Scaglione, M., and Indelli, P.F. (2018). Giovanni Alfonso Borelli: The precursor of medial pivot concept in knee biomechanics. Joints, 6:167–172.
Primus, M.A. (2022). Social tensegrity and family systems. Journal of Human Behavior in the Social Environment, 34:210–220.
Profeta, V.L.S., Turvey, M.T., and Carello, C. (2020). Goal-directed action and the architecture of movement organization. In: M.L. Latash, ed. Berstein’s construction of movements. Routledge.
Reilly, C.B., and Ingber, D.E. (2018). Multi-scale modeling reveals use of hierarchical tensegrity principles at the molecular, multi-molecular, and cellular levels. Extreme Mechanics Letters, 20:21–28.
Reznikov, N., Chase, H., Ben Zvi, Y., Tarle, V., Singer, M., Brumfeld, V., Shahar, R., and Weiner, S. (2016). Inter-trabecular angle: A parameter of trabecular bone architecture in the human proximal femur that reveals underlying topological motifs. Acta Biomaterialia, 44:65–72.
Rimoli, J.J., and Pal, R.K. (2017). Mechanical response of 3-dimensional tensegrity lattices. Composites Part B: Engineering, 115:30–42.
Rivier, N., Sadoc, J.F., and Charvolin, J. 2016. Phyllotaxis: a framework for foam topological evolution. European Physical Journal E, 39:1–11.
Robbie, D.L. (1977). Tensional forces in the human body. Orthopaedic Review, 6:45–48.
Russell, B. (2009). The scientific outlook. Oxford: Routledge.
Sadoc, J.F., and Rivier, N. (2000). Boerdijk–Coxeter helix and biological helices as quasicrystals. Materials Science and Engineering: A, 294–296:397–400.
Saxena, A., Lipson, H., and Valero-Cuevas, F.J. (2012). Functional inference of complex anatomical tendinous networks at a macroscopic scale via sparse experimentation. PLoS Computational Biology, 8:e1002751.
Scarr, G. (2008). A model of the cranial vault as a tensegrity structure and its significance to normal and abnormal cranial development. International Journal of Osteopathic Medicine, 11:80–89.
Scarr, G. (2012). A consideration of the elbow as a tensegrity structure. International Journal of Osteopathic Medicine, 15:53-65. Scarr, G. (2016). Fascial hierarchies and the relevance of crossed-helical arrangements of collagen to changes in the shape of muscles. Journal of Bodywork and Movement Therapies, 20:377-387.
Scarr, G. (2018). Biotensegrity: the structural basis of life. second ed. Edinburgh: Handspring.
Scarr, G. (2020). Biotensegrity: what is the big deal? Journal of Bodywork and Movement Therapies, 24:134–137.
Scarr, G. (In press). Movement is a whole-body issue., In: E, Larkam, and M, Black, eds. Pilates applications for health conditions, volume 1., Handspring.
Scarr, G., and Harrison, H. (2016). Resolving the problems and controversies surrounding temporo-mandibular mechanics. Journal of Applied Biomedicine, 14:177–185.
Scarr, G., and Harrison, H. (2017). Examining the temporo-mandibular joint from a biotensegrity perspective: A change in thinking. Journal of Applied Biomedicine, 15:55–62.
Scarr, G., Blyum, L., Levin, S.M., and de Solórzano, S.L. (2024). Moving beyond Vesalius: Why anatomy needs a mapping update. Medical Hypotheses, 183:111257.
Schrödinger, E. (1944). What is life? Cambridge: Cambridge University Press.
Serón, F.J., Zaldívar, Á., Blesa, A., Celani, G., and Magallón, J. (2022). A theoretical reflection on smart shape modeling. International Journal on Interactive Design and Manufacturing, 16:821–839.
Sitharam, M., and Agbandje-Mckenna, M. (2006). Modeling virus self-assembly pathways: avoiding dynamics using geometric constraint decomposition. Journal of Computational Biology, 13: 1232–1265.
Skelton, R.E., Helton, W.W., Chan, W., Pinaud, J.-P., and Adhikari, R. (2001). An introduction to tensegrity structures. Proceedings of the 40th IEEE Conference on Decision and Control, 1–6.
Snelson, K. (1996). Snelson on the tensegrity invention. International Journal of Space Structures, 11:43–48.
Stamenović, D., and Smith, M.L. (2020). Tensional homeostasis at different length scales. Soft Matter, 16:6946-6963.
Standring, S. (2005). Gray’s anatomy. 39th ed. Edinburgh: Elsevier Churchill Livingstone.
Tadeo, I., Berbegall, A.P., Escudero, L.M., Álvaro, T., and Noguera, R. (2014). Biotensegrity of the extracellular matrix: Physiology, dynamic mechanical balance, and implications in oncology and mechanotherapy. Frontiers in Oncology, 4:39.
Terayama, K., Takei, T., and Nakada, K. (1980). Joint space of the human knee and hip joint under a static load. Engineering in Medicine, 9:67–74.
Thompson, D.W. (1917). On growth and form. Cambridge: Cambridge University Press.
Turvey, M.T., and Fonseca, S.T. (2014). The medium of haptic perception: a tensegrity hypothesis. Journal of Motor Behavior, 46:143–187.
Valero-Cuevas, F.J., Yi, J.-W., Brown, D., McNamara, R. V, Paul, C., and Lipson, H. (2007). The tendon network of the fingers performs anatomical computation at a macroscopic scale. IEEE Transactions on Biomedical Engineering, 54:1161–1166.
Van Essen, D.C. (2023). Biomechanical models and mechanisms of cellular morphogenesis and cerebral cortical expansion and folding. Seminars in Cell and Developmental Biology, 140:90-104.
Vesalius, A. (1543). De humani corporis fabrica. Padua: University of Padua.
Wilke, J., Schleip, R., Yucesoy, C.A., and Banzer, W. (2018). Not merely a protective packing organ? A review of fascia and its force transmission capacity. Journal of Applied Physiology, 124:234–244.
Wilson, J., and Kiely, J. (2016). The multi-functional foot in athletic movement: extraordinary feats by our extraordinary feet. Human Movement, 17:15-20.
Witztum, A., and Wayne, R. 2014. Fibre cables in the lacunae of Typha leaves contribute to a tensegrity structure. Annals of Botany, 113:789–797.
Yang, Q., Cao, M., and Anderson, B.D.O. 2019. Growing super stable tensegrity frameworks. IEEE Transactions on Cybernetics, 49:2524–2535.
Ziauddin, M., and Ali, B. 2013. An ultrasonic study on elasticity of animal soft tissues. International Journal of Science, Environment and Technology, 2:1257–1261.
